初等函数在定义区间内一定连续吗(初等函数在定义区间内一定连续吗为什么)

一切初等函数在其「定义区间」内都是连续的。

定义区间，顾名思义，在某个区间上的函数都是有定义的。孤立的点构不成区间。

“初等函数在其定义区间内可导”这句话是错的。y=|x|=√(x^2),这是一个初等函数，定义区间为（-∞，+∞），但在x=0处是不可导的。

高等数学中提到初等函数在定义区间（不是定义域）一定连续，函数如果在某些孤立的点有定义，那么这些点是在其定义域内的，但是这些孤立的点是不在其定义区间内的。

总结就是：基本初等函数在其定义域内连续；初等函数在其定义区间内连续。

初等函数简介：

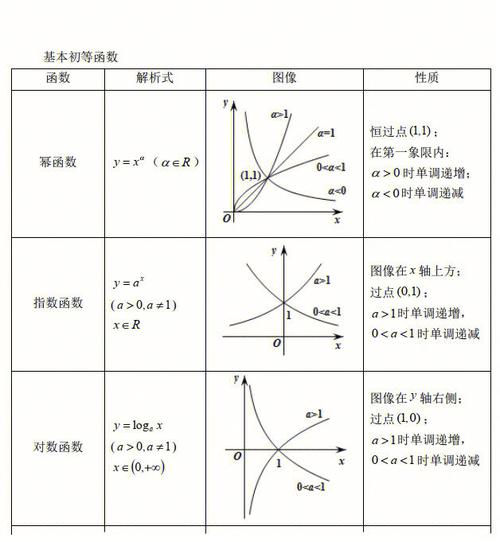
由幂函数（powerfunction）、指数函数（exponentialfunction）、对数函数（logarithmicfunction）、三角函数（trigonometricfunction）。

反三角函数（inversetrigonometricfunction）与常数经过有限次的有理运算（加、减、乘、除、有理数次乘方、有理数次开方）及有限次函数复合所产生，并且能用一个解析式表示的函数。

初等函数在定义区间内一定连续吗为什么

求极限的时候什么情况下可以直接带入：初等函数在定义区间内连续,因此初等函数定义域内的点都可以直接代入求得极限。

初等函数介绍如下：

初等函数是由幂函数（powerfunction）、指数函数（exponentialfunction）、对数函数logarithmicfunction、三角函数（trigonometricfunction）。

还有一系列双曲函数也是初等函数，如sinh的名称是双曲正弦或超正弦，cosh是双曲余弦或超余弦，tanh是双曲正切，coth是双曲余切，sech是双曲正割，csch是双曲余割。

初等函数在其定义区间内一定连续。

有理函数介绍如下：

实系数多项式称为整有理函数。其中最简单的是线性函数y=α0+α1x，它的图象是过y轴上y=α0点的斜率为α1的直线。二次整有理函数y=α0+α1x+α2x2的图象为抛物线。

两个整有理函数之比为分式有理函数。分式有理函数其中最简单的是反比例函数，其图象为双曲线。整有理函数和分式有理函数统称有理函数。有理函数起源于代数学。

极限介绍如下：

极限是数学中的分支——微积分的基础概念，广义的“极限”是指无限靠近而永远不能到达的意思。

数学中的“极限”指：某一个函数中的某一个变量，此变量在变大或者变小的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”。