初等函数怎么判断(初等函数怎么判断是否可导)

可以观察此函数是否是由基本初等函数经过有限的四则运算变形而来的。因为由基本初等函数经过有限次的四则运算以及有限次的复合所生成的函数称为初等函数。

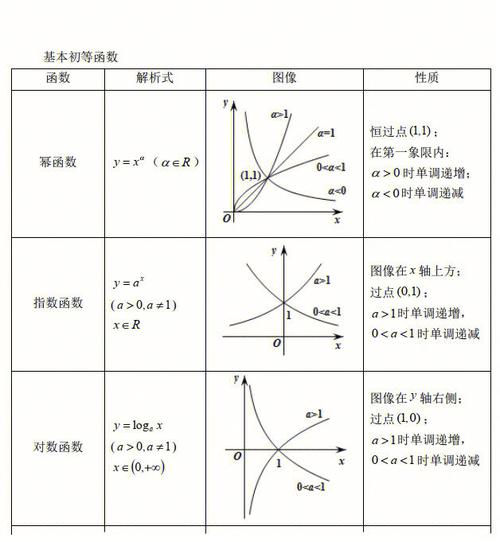
基本初等函数有：常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。

举例举例说：e的x次方为初等函数，这是基本初等函数，e的x次方+x的平方，是初等函数，这是两个基本初等函数的和，e的x次方*x的平方，这也是初等函数，这是两个基本初等函数的积，甚至e的（x的平方）次方也是初等函数。

函数的由来：

中文数学书上使用的“函数”一词是转译词。是我国清代数学家李善兰在翻译《代数学》（1859年）一书时，把“function”译成“函数”的。

中国古代“函”字与“含”字通用，都有着“包含”的意思。

李善兰给出的定义是：“凡式中含天，为天之函数。

”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量。

这个定义的含义是：“凡是公式中含有变量x，则该式子叫做x的函数。

”。

所以“函数”是指公式里含有变量的意思。我们所说的方程的确切定义是指含有未知数的等式。但是方程一词在我国早期的数学专著《九章算术》中，意思指的是包含多个未知量的联立一次方程，即所说的线性方程组。

初等函数怎么判断是否可导

不一定。

初等函数在其定义区间内不一定可导，如f(x)=x.f(x)=x也是初等函数。

初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数、与常数经过有限次的有理运算，加、减、乘、除、有理数次乘方、有理数次开方及有限次函数复合所产生，并且能用一个解析式表示的函数。

即基本初等函数经过有限次的四则运算或有限次的函数复合所构成并可以用一个解析式表出的函数，称为初等函数。

一个初等函数，除了可以用初等解析式表示以外，往往还有其他表示形式。

初等函数是最先被研究的一类函数，它与人类的生产和生活密切相关，并且应用广泛。

为了方便，人们编制了各种函数表，如平方表、开方表、对数表、三角函数表等。

一切初等函数在其「定义区间」内都是连续的。

定义区间，顾名思义，在某个区间上的函数都是有定义的。

孤立的点构不成区间。

“初等函数在其定义区间内可导”这句话是错的。

y=x=√(x^2)，这是一个初等函数，定义区间为（-∞，+∞），但在x=0处是不可导的。

高等数学中提到初等函数在定义区间（不是定义域）一定连续，函数如果在某些孤立的点有定义，那么这些点是在其定义域内的，但是这些孤立的点是不在其定义区间内的。

总结就是：基本初等函数在其定义域内连续；初等函数在其定义区间内连续。