初等函数是什么

初等函数是指那些通过有限次的四则运算（加、减、乘、除）和复合运算，从常数、幂函数、指数函数、对数函数、三角函数以及反三角函数中构建出来的函数。

这些函数能够用一个明确的数学表达式来表示，这使得它们在数学分析、工程学、物理学等领域具有广泛的应用。

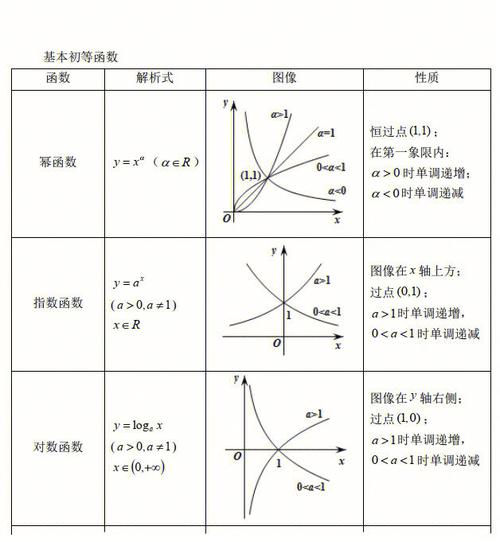
幂函数是一类非常基础的初等函数，它的一般形式为f(x)=x^n，其中n为常数。

指数函数则具有形如f(x)=a^x的形式，其中a是大于零且不等于1的常数。

对数函数则可以表示为f(x)=log_a(x)，其中a也是大于零且不等于1的常数。

三角函数包括正弦、余弦和正切等，它们分别用sin(x)、cos(x)和tan(x)来表示。

反三角函数则是三角函数的逆函数，如arcsin(x)、arccos(x)和arctan(x)。

初等函数因其简洁明了的表达方式和强大的数学工具属性，成为了数学分析和工程应用中的基础工具。

通过它们的组合与变换，可以构建出描述各种复杂现象的数学模型。

这些函数不仅在理论研究中发挥着重要作用，也在实际应用中展现出广泛的适用性，从物理系统的建模到经济预测，从信号处理到控制系统设计，初等函数都扮演着不可或缺的角色。

在数学中，初等函数的定义和性质是理解更复杂数学概念的基础。

通过对这些基本函数的学习和掌握，学生能够更好地理解和应用更高阶的数学理论和方法。

同时，初等函数的广泛应用也体现了数学在现代社会中的重要地位，展示了数学作为一门科学的力量和魅力。

基本初等函数是什么

基本初等函数是数学分析的基础，主要包括五类：常数函数、幂函数、指数函数、对数函数以及三角函数和反三角函数。

常数函数是最简单的函数形式，其定义为y=c（c为常数），无论x取何值，函数值始终为c。

幂函数则定义为y=x^a（a为常数），其图形随a值的不同而变化，当a为正整数时，图形为向上开口的抛物线；当a为负整数时，图形为双曲线。

指数函数是一种特殊形式的幂函数，其定义为y=a^x（a>0,a≠1），其中底数a是一个正实数且不等于1，这种函数的增长或衰减速度与a的大小密切相关。

对数函数是指数函数的逆运算，其定义为y=log_ax（a>0,a≠1，x>0），函数的定义域为（0，+∞），即x>0。

指数函数里对于底数a的规定，同样适用于对数函数。

三角函数与反三角函数是处理角度和周期性现象的关键工具。常见三角函数包括正弦（y=sinx）、余弦（y=cosx）、正切（y=tanx）等，它们描述了直角三角形中边长与角度之间的关系。

反三角函数则是三角函数的逆运算，如反正弦（y=arcsinx）、反余弦（y=arccosx）、反正切（y=arctanx）等，它们用于确定给定比值对应的角。

幂函数、指数函数、对数函数、三角函数和反三角函数在数学中扮演着重要角色，广泛应用于科学、工程、经济学等领域。

幂函数一般形式为y=x^α（α为常数），可以是自然数、有理数或任意实数、复数。

指数函数的一般形式为y=a^x（a>0,a≠1），其中底数a是一个正实数且不等于1。

对数函数则为y=log_ax（a>0,a≠1，x>0），特别当α=e时，记为y=lnx。

三角函数和反三角函数是周期性的，正弦、余弦、正切等函数的周期性使得它们非常适合描述周期性的物理现象，如波动、旋转等。