阿尔法、贝塔、伽马符号分别是α、β、&gamma。
详细解释如下:
在数学、物理、工程等领域,我们常常会遇到各种符号,其中阿尔法、贝塔、伽马是常见的符号之一。这些符号都有各自特定的用途和含义。
1.阿尔法:是希腊字母中的第一个字母,通常用来表示角的度数值或者其他数学常数。在物理学中,阿尔法粒子是一个重要的概念,指的是放射性元素放射出的高能粒子。
2.贝塔:也是希腊字母,通常用来表示变量或者特征值。在统计学和机器学习领域,贝塔分布是一个常见的概率分布,用于描述一组数据的分布情况。此外,贝塔函数在数学中也有特定的定义和应用。
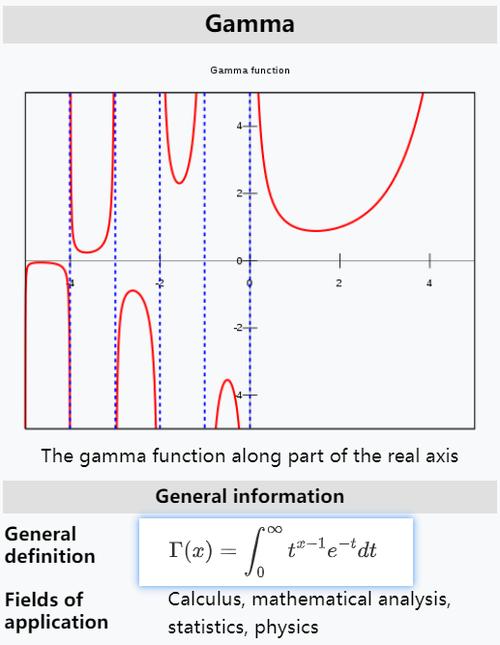
3.伽马:同样是希腊字母,在数学中常用来表示射线的符号。在物理学中,伽马射线是一种高能电磁波,具有很强的穿透能力。此外,伽马函数也是一种重要的数学函数,广泛应用于概率论、量子力学等领域。
这三个符号在不同的学科领域中具有不同的含义和应用,但都承载着重要的信息和意义。随着对这些领域的深入学习和研究,我们会更加熟悉这些符号的用途和含义。
gamma函数的表达式
了解Gamma函数的由来,我们首先回顾阶乘的定义:n!=n×(n-1)×...×1,其中n为正整数。阶乘的定义被拓展至复数域时,形成了新的概念,即Gamma函数。
Gamma函数定义如下:Γ(n)=(n-1)!对于所有复数n,且当n>0时,满足Γ(n)=(n-1)Γ(n-1)的递推关系。这个定义能够延伸至非整数及复数。
Gamma函数的直观理解在于它提供了一种将积分与阶乘联系起来的方式。
以Γ(n)为例,可以写作Γ(n)=∫_0^∞t^(n-1)e^(-t)dt。
这个积分形式揭示了Gamma函数与指数函数及指数分布之间的关系。
Gamma函数满足递推公式Γ(n)=(n-1)Γ(n-1),这个性质使得计算Gamma函数值变得简便。例如,当n为整数时,可以通过连续应用递推公式来得到阶乘形式的表达式。
一个重要的余元公式是:Γ(n+1)=nΓ(n),从这个公式出发,可以推导出当n为正整数时,Γ(n)=(n-1)!,即Gamma函数在正整数上与阶乘函数相等。
综上所述,Gamma函数不仅提供了阶乘在复数域的推广,而且在数学分析中扮演着重要角色,尤其是在积分和概率论中。通过理解其定义、性质和应用,我们能够更深入地掌握Gamma函数的含义和用途。







还没有评论,来说两句吧...