初等函数在定义域内一定连续吗

讨论初等函数在其定义域内的连续性，首先要澄清概念。

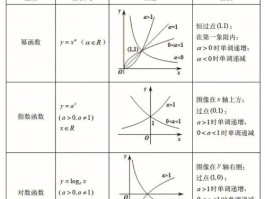
初等函数是通过有限次基本运算（加、减、乘、除、幂、根、对数、三角）组合得到的函数，如线性函数、二次函数、指数函数、对数函数、三角函数等。

这些函数在数学分析中占有重要地位，其定义域往往为实数集。

初等函数在其定义域内连续性的本质，在于函数值与自变量值之间的关系。

若对于任意点\(a\)在函数\(f(x)\)的定义域内，当\(x\)无限接近于\(a\)时，\(f(x)\)的值无限接近于\(f(a)\)，则称\(f(x)\)在点\(a\)处连续。

连续性概念的直观含义是：在函数图象上，若无“跳跃”或“断点”，则函数在该点连续。

对于初等函数而言，由于它们的定义和性质，大部分情况下在定义域内是连续的。

例如线性函数\(f(x)=ax+b\)，二次函数\(f(x)=ax^2+bx+c\)，指数函数\(f(x)=a^x\)，对数函数\(f(x)=\log_ax\)，三角函数\(f(x)=\sinx\)，等等。

这些函数的连续性主要依赖于其基本运算的连续性和函数性质。

例外出现在函数定义域内的某些特殊点，如分段函数的接点、根号函数中的负数下标、某些分式函数的分母为零点等。

在这些点，若函数在该点左右两侧的极限存在且相等，则函数在该点连续。

若极限存在但不等于函数值，或极限不存在，则函数在该点不连续。

总结而言，初等函数在其定义域内通常连续，但需要根据函数的具体形式和定义域内的点性质来具体分析。

对于孤立点或极限点，连续性的判断需遵循定义并结合函数行为。

总体而言，初等函数连续性的判断遵循基本的数学分析原理，无需过分复杂化。