初等函数(初等函数导数)

初等函数怎么判断如下：

1.由基本初等函数经过有限次的四则运算、代入、求导后得到的新函数，仍是初等函数。

2.用加、减、乘、除、求幂、求对数等有限次组合初等函数，可以得到的函数仍是初等函数。

3.如果一个函数有反函数，且反函数也是初等函数，则该函数为初等函数。

4.任意初等函数在其定义域的任一点的极限也可由初等函数表示，则该函数为初等函数。

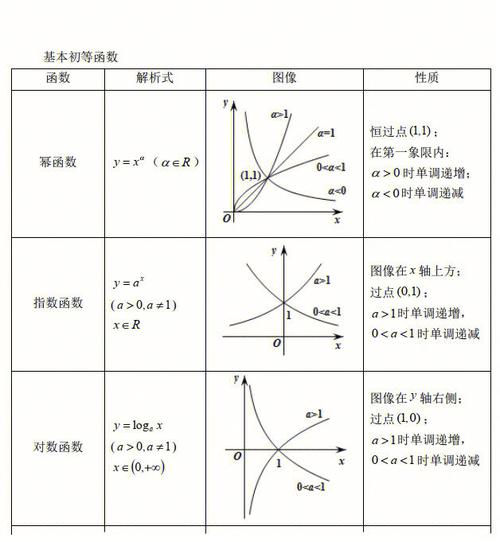
初等函数是数学中的一个重要概念，指的是由基本初等函数经过有限次的四则运算和复合运算得到的函数。基本初等函数包括幂函数、指数函数、对数函数、三角函数和反三角函数等。

初等函数具有一些基本性质，如封闭性、连续性、可导性、可积性等。

这些性质在研究函数的性质、变化率和优化等问题时非常重要。

例如，函数的单调性和极值可以通过函数的导数来研究，函数的积分可以通过函数的原函数来求解。

初等函数的表达形式有四种基本类型：幂函数、指数函数、对数函数和三角函数。

幂函数是指形如y=x^n的函数，指数函数是指形如y=a^x的函数，对数函数是指形如y=log_ax的函数，三角函数是指形如y=sinx、y=cosx或y=tanx等以三角关系式为基础的函数。

初等函数在实际应用中有着广泛的应用，如物理、工程、经济等领域。例如，物理学中的牛顿第二定律F=ma，流体力学中的伯努利方程等都涉及到初等函数的运用。

在工程领域，初等函数可以用于描述电路的电压、电流和电阻之间的关系，用于描述机械系统的运动规律和动力学特征等。

在经济学领域，初等函数可以用于描述商品的需求量和价格之间的关系，用于描述企业的成本和收益之间的关系等。

总之，初等函数是数学中的一个重要概念，具有广泛的应用价值。通过学习和掌握初等函数的基本概念和性质，我们可以更好地理解和解决实际问题，提高自己的数学素养和科学素养。

初等函数导数

数学所有的求导公式如下

基本初等函数的导数表

y=cy'=0、y=α^μy'=μα^(μ-1)、y=a^xy'=a^xlna、y=e^xy'=e^x、y=loga,xy'=loga,e/x、y=lnxy'=1/x、y=sinxy'=cosx、y=cosxy'=-sinx、y=tanxy'=(secx)^2=1/(cosx)^2、y=cotxy'=-(cscx)^2=-1/(sinx)^2、。

y=arcsinxy'=1/√(1-x^2)、y=arccosxy'=-1/√(1-x^2)、y=arctanxy'=1/(1+x^2)、y=arccotxy'=-1/(1+x^2)、y=shxy'=chx、y=cxy'=shx、y=thxy'=1/(chx)^2、y=arshxy'=1/√(1+x^2)、y=archxy'=1/√(x^2-1)、y=arthy'=1/(1-x^2)。

求导公式

c'=0(c为常数）、(x^a)'=ax^(a-1),a为常数且a≠0、(a^x)'=a^xlna、(e^x)'=e^x、(logax)'=1/(xlna),a>0且a≠1、(lnx)'=1/x、(sinx)'=cosx、(cosx)'=-sinx、(tanx)'=(secx)^2、(secx)'=secxtanx、。

(cotx)'=-(cscx)^2、(cscx)'=-csxcotx、(arcsinx)'=1/√(1-x^2)、(arccosx)'=-1/√(1-x^2)、(arctanx)'=1/(1+x^2)、(arccotx)'=-1/(1+x^2)、(shx)'=chx、(chx)'=shx、(uv)'=uv'+u'v、(u+v)'=u'+v'、(u/)'=(u'v-uv')/^2。