纳什均衡,这个博弈论中的关键概念,以约翰·纳什的名字命名,是描述非合作博弈中的一种稳定策略组合。
它表明在给定的策略组合下,无论单个参与者如何改变策略,都无法从中获得更好的结果。
纳什均衡的定义在经济学和数学上有所不同,但核心思想是所有参与者在固定策略下不会改变。
在纳什的理论中,例如两家公司价格战的例子,如果一方不改变策略,另一方降价或提价都无法增加收益,这就形成一个僵局,即纳什均衡。
同样,选举、群体冲突等场景也能应用这个理论。
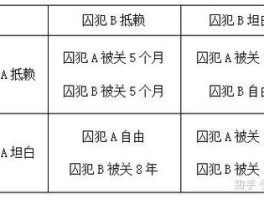
纳什均衡案例丰富多样,如囚徒困境、智猪博弈、商业博弈等。
在囚徒困境中,两个嫌疑人为了各自利益最大化,结果可能双输,这就是一个纳什均衡。
智猪博弈中,小猪选择搭便车,大猪疲于奔命,也是纳什均衡的体现。
在企业竞争中,若双方都选择背叛策略,形成“囚徒困境”,但若博弈次数无限,双方会趋向于合作,达到双赢的(3,3)收益,这也是一个纳什均衡。
至于硬币游戏,美女提出的条件形成了一种混合策略纳什均衡,无论你采取何种策略,美女的期望收益都是固定的。这个例子表明,即使看似复杂的游戏,也可能存在明确的策略组合,构成纳什均衡。
纳什均衡的存在和分析,不仅在经济学中具有重要意义,也扩展到了日常生活的诸多领域,它强调了在复杂互动中,各方策略的相互依赖和动态平衡。
纳什均衡理论的意义和价值
纳什均衡是指在博弈中,每一参与者都无法通过单方面改变自身策略来改善其支付的情形。
接下来详细解释纳什均衡的概念:
首先,纳什均衡是建立在博弈理论的一个核心概念之上的。
在博弈中,参与者都拥有各自可选择的策略,并且每种策略组合都对应着一种特定的收益或支付。
当所有参与者所选择的策略组合达到了这样的一种状态:在此状态下,任何一位参与者都无法通过单方面改变策略来获得更高的支付,这种状态就被称为纳什均衡。
简单地说,纳什均衡是博弈中的稳定状态,因为任何单方面改变策略的行为都不会带来更好的结果。
其次,从数学角度来看,纳什均衡体现了博弈策略的最优选择。
在有限的策略集合中,参与者选择的策略是最优的,意味着他们无法通过改变策略来获得更高的效用或支付。
这种状态是博弈的均衡点,没有任何参与者愿意主动改变策略。
这种均衡的实现基于所有参与者的理性决策,即他们都会根据自己的最优判断来选择策略。
最后,纳什均衡在经济学、政治学、社会学等多个领域都有广泛的应用。
在经济市场的竞争中,企业之间的策略选择可能达到纳什均衡状态,任何一方都难以通过单一策略的改变来占据更大市场份额或获取更多利润。
在政治谈判或国际关系中,各方也可能通过谈判和协商达到某种纳什均衡,使得冲突得以避免或达到某种平衡状态。
因此,纳什均衡是博弈理论中的重要概念,它描述了博弈中参与者策略选择的稳定状态,这种状态在任何单方面改变策略的情况下都不会被打破。









还没有评论,来说两句吧...