纳什均衡解决囚徒困境

囚徒困境是博弈理论中的一个经典问题，涉及到合作与背叛的问题。

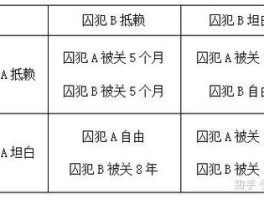
在这个问题中，两个罪犯被分开审问，如果他们都保持沉默，则可以被判轻罪；如果其中一人供出另一个，则供出者将被判轻罪，而另一个将被判重罪；如果两人都供出对方，则两人都将被判重罪。

该问题中的关键在于合作与背叛的权衡，解决该问题就要从多个角度分析。

如何解决囚徒困境

第一，从心理学角度分析，囚徒困境的出现是因为双方都希望自己最后获得最大利益，而无法信任对方。

这种心理难以打破，所以需要引入第三方机构或者制度来平衡游戏。

比如，可以设立奖励机制，鼓励双方达成合作；也可以设立惩罚机制，惩罚背叛者，同时给予合作者更多的奖励。

第二，从经济学角度分析，囚徒困境问题与市场经济中的信息不对称问题有些类似。

而像信息公开等机制可以解决信息不对称问题一样，也可以在囚徒困境问题中引入信息公开，让双方均了解到合作所可能获得的利益，从而达成合作。

第三，从政治学角度分析，囚徒困境问题实际上类似于国际贸易谈判中的一些情况。

在这种情况下，要达成合作，需要充分了解对方的诉求和利益，并进行妥善协商。

同时，在协商过程中，还需要依托一些国际组织或者国家力量，对游戏进行引导和约束。

最后，解决囚徒困境的方法也需要考虑到实际情况。在游戏理论中，囚徒困境存在唯一的纳什均衡，即双方都背叛对方。但在实际情况中，双方还需要考虑到长期利益和道德信仰等问题，而不能仅仅追求一时的利益。

纳什均衡囚徒困境矩阵的形式

本章将探讨策略互动在多决策者环境中的应用，博弈论成为核心工具。深入理解博弈论的起点，我们首先概述其基本概念。

博弈论涉及三个关键概念：参与者、策略和支付。

参与者可以是个人或组织，他们的选择构成策略集，而支付则衡量参与者的收益。

在两方博弈中，例如参与者1和2的互动，策略集[公式]和[公式]分别代表每个参与者的选择，支付[公式]描述选择策略[公式]和[公式]的结果。

纯策略纳什均衡是博弈中的关键概念，它定义为即使面对对手策略，每个参与者都没有改变当前策略的动力。

在两方博弈中，若给定[formula]，[formula]不可能有更高收益的[formula]，反之亦然。

这表明在均衡状态下，任何一方改变策略都无法提高其收益。

通过数学定义，纳什均衡要求每个参与者在对手策略确定时，其最佳策略就是当前策略。

例如，对于任意[formula]，最优反应函数定义了参与者在给定情况下最优的策略选择。

纳什均衡在矩阵形式中通过划线法寻找，如在囚徒困境和夫妻博弈中所展示的。

在夫妻博弈中，双方的决策选择构成一个非唯一纳什均衡，可能有多种结果，表明博弈论揭示出策略互动的复杂性。博弈论分析帮助我们理解在各种情境中，参与者如何平衡和权衡自身的利益，寻找最优策略。