博弈论是什么意思

1、博弈论又被称为对策论,它是现代数学的一个新分支，也是运筹学的一个重要组成内容。

按照2005年因对博弈论的贡献而获得诺贝尔经济学奖的RobertAumann教授的说法，博弈论就是研究互动决策的理论。

所谓互动决策，即各行动方（即局中人)的决策是相互影响的，每个人在决策的时候必须将他人的决策纳入自己的决策考虑之中，当然也需要把别人对于自己的考虑也要纳入考虑之中……在如此迭代考虑情形进行决策，选择最有利于自己的战略。

2、通俗点说，就是不同方面策略的组合互动，对于一件事，你有几种不同的策略，别人也有几种，对你最有利的不一定是对别人最有利的，你就不能简单的根据自己的观点进行选择，所以你会在考虑别人选择的情况下，选择你自己的策略。

举个简单的例子，两个公司都将生产一种新产品，如果两人同时生产获利为1，如果只有一家生产，生产的获利为3，不生产的获利为0，如果都不生产双方获利为2。

那么作为两家厂家在互相不知道对方策略情况下选择如何生产，就是在博弈。

博弈在生产，行业进入，特别是在垄断形态下的市场中运用很广。

时间博弈论是什么意思

本文将深入探讨博弈的分类及组成要素，旨在为读者提供对博弈论核心概念的全面理解。

博弈论的分类主要从不同角度展开。

首先，从博弈者出招的顺序、持续时间和重复次数，我们可将博弈分为静态博弈和动态博弈。

静态博弈是指所有参与者同时做出决策，而动态博弈中，决策者会依据前者的策略做出自己的选择。

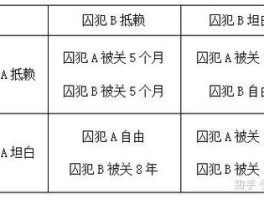
例如，囚徒困境便展示了静态博弈的典型情形，其中一方行动后，另一方并未得知对方选择，只能基于自身利益做出判断。

其次，根据信息透明度，博弈可分为完全信息博弈和不完全信息博弈。

在完全信息博弈中，所有参与者都对其他人的特征、策略空间及收益有全面了解；不完全信息博弈中，参与者对部分信息掌握不全，需通过概率和推断作出决策。

确定的博弈与不确定的博弈则关注信息是否为确定性。

对称信息博弈与非对称信息博弈则侧重于参与者之间信息的对称性。

博弈的另一个分类依据为参与者间的合作关系，分为合作博弈和非合作博弈。合作博弈中，参与者通过协议约束策略，共同追求目标，而非合作博弈则无此约束。

收益情况分类则将博弈分为零和博弈、非零和博弈、常和博弈及变和博弈。

零和博弈中，一方的收益总是以另一方的损失为代价。

非零和博弈中，各参与者收益之和并非恒定，可能增加或减少。

常和博弈的总收益保持不变，而变和博弈中，总收益随策略变化。

参与方角色包括单人博弈、双人博弈和多人博弈。单人博弈简化为优化问题，双人博弈如猜硬币游戏、囚徒困境等广泛存在，多人博弈则更加复杂，可能涉及“破坏者”策略。

策略方面，策略空间指的是参与者可选择的全部策略集合，有限次博弈和无限次博弈则取决于策略数量的可数性。收益矩阵和收益函数用于表示不同博弈情况下的收益。

博弈过程分为静态博弈、动态博弈和重复博弈。静态博弈要求同时决策，动态博弈中决策有先后顺序，而重复博弈则指同一博弈多次进行。重复博弈的性质与动态博弈相似，且大多数重复博弈也是静态博弈的组合。

理解这些分类及组成要素对于深入研究博弈论及其应用至关重要，通过不同角度的分析，可以更准确地预测和解决复杂决策问题。

参考文献：博弈论（范如国）