纳什均衡解的计算(求解纳什均衡的方法有哪些)

原文发布于自己的博客平台【http://www.jetchen.cn/nash-equilibrium/】

具有竞争或对抗性质的行为称为博弈行为，并且博弈理论在经济学、国际关系、军事战略等很多领域都有广泛的应用，其中以纳什均衡为代表的非合作性博弈理论在日常中最为常用。

在很多场景下，比如玩德州扑克等游戏时，虽然有些时候选择的策略并不一定是全局的最优解，但却是相对于其他人的策略而做出的最优解，即每个人都是对自己最有利的解决方案，我们将其称为为纳什均衡。

纳什均衡（或者纳什平衡），Nashequilibrium，又称为非合作博弈均衡，是博弈论的一个重要策略组合，以约翰·纳什命名。

再解释一下，所谓纳什均衡，指的是参与者的一种策略组合，在该策略上，任何参与人单独改变策略都不会得到好处，即每个人的策略都是对其他人的策略的最优反应。

换句话说，如果在一个策略组合上，当所有其他人都不改变策略时，没有人会改变自己的策略，则该策略组合就是一个纳什均衡。

枯燥的描述很难理解，下面使用几个案例来理解下。

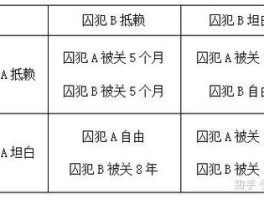
背景：有两个囚犯A和B，犯事儿进去了，然后警官对其分开审讯，所以A和B是没有机会进行串供的。

奖惩：如果双双招供，则各判2年，如果双双不招供，则各判1年，如果一个招供一个不招供，则招供的人立即释放，不招供的人判刑十年。

结果：最后囚犯A和B都会选择招供，所以各判2年，这个便是此时的纳什均衡。

但是明明双双不招供才是最优解啊，其实不然，回头再看一下概念，纳什均衡其实并不是全局的最优解，而是每个人相对于每个人的策略而做出的最佳策略，下面来解释下。

我们来建立一个数学模型，使用-2、-1、0、-10来形容上面的奖惩，见下面的分析图。

A的心路历程：

所以，不管B招不招供，A只要招供了，对A而言是最优的策略。

同理，对于B的心路历程也相似，B也会选择招供：

所以最终的结果是A和B都选择了招供。

即此时的纳什均衡点为：A和B都招供。

综述，敲黑板，纳什均衡的前提是：决策圈中的个体是独立，不合作，不横向沟通的。

背景：有两只猪，一只是大猪，另一只是小猪，然后有一个食槽，里面会有食物落下，但是需要去远处按一下按钮，每次按一下按钮，食槽中便会补满食物。但是呢，在按按钮的来回路上，是需要消耗一定的能量的。

奖惩：跑过去按一下按钮再跑回来吃食物，会消耗一些能量，记为-2，每次食槽中补满食物，总食物量为10份，大猪先吃的话能吃到9份，小猪先吃的话，大猪能吃到6份，一起吃的话，大猪能吃到7份

结果：大猪会选择去按按钮，而小猪会选择不去按按钮，即在原地等着。

小猪心路历程：

所以，不管大猪怎么样，小猪都会选择在原地等待。

大猪心路历程：

所以，表面上看，大猪的决策是受到小猪的决策所影响的，但是分析小猪的心路历程得知，小猪是不会去按按钮的，那么大猪最后的决策还是会选择去按按钮，这样大猪的收益才会最大化。

所以综上，最终结果是大猪去按按钮，而小猪在原地等待着。

即此时的纳什均衡点为：大猪去，小猪不去。

在每次参与者都只有有限种策略选择并且允许混合策略的前提下，纳什均衡是一定存在的。

比如选举、群体之间的利益竞争、会议中的法案竞争等，是必然存在纳什均衡的。

以公司间的价格战为例：如果对方一直降价，那我方继续降价必然会出现亏本买卖，然而如果不降价，也会出现失去市场的情况，损失更大，但如果对方不降价，我方更要降价才能谋得一丝丝利益，所以只要出现价格战，必然会两败俱伤，这是纳什均衡体现的必然结局。

所以要改变这种结局，双方必须坐下来谈判寻求新的利益评估分摊方案，从而改变原先的利益格局（比如当年京东和当当的一场价格战，最终以双方各占某一方面的主市场从而获得新的利益分割方案）。

纳什均衡是基于非合作博弈论的平衡不动点解

例如上文的囚徒困境问题，如果两个囚徒是有合作的，则必然不存在纳什均衡点。

所以，在现实生活中，纳什均衡这一博弈是很重要但是也是很有限的，因为在很多情况下，即使知道平衡不动点必然存在，但是往往却很难找到。

纳什均衡（这一非合作博弈论模型）仅仅是突破了博弈论中的一个局限。

因为在社会这一庞大的博弈环境下，还会掺杂着复杂的经济行为，虽然社会中的大家并非是集体合作性的，但在这种庞大的非合作性对象中，纳什均衡点是几乎不可能找到的。

纳什均衡属于NP问题

（摘自wiki上面的一段话，暂时看不懂但却觉得很有道理）纳什均衡属于NP问题，Daskalakis证明它属于NP问题的一个子集，不是通常认为的NP-完全问题，而是PPAD-完全问题。

这项研究成果被一些计算机科学家认为是十年来博弈论领域的最大进展。

求解纳什均衡的方法有哪些

博弈论进阶：探索纳什均衡的世界</

在博弈论的舞台上，每一步决策都如同一场智慧的较量。

在上一章中，我们简要回顾了博弈的基本元素，如最优响应和受控行动。

但今天，我们将深入探讨纳什均衡，这是博弈理论的核心概念，它揭示了在复杂的交互决策中，各方如何找到一个动态平衡点。

首先，让我们通过B/C博弈来理解最优响应的概念。

在这个博弈中，玩家1面对两种可能的对手行动，通过计算和分析，找到在不同情况下自己的最优策略。

在这个过程中，我们引入了纯策略纳什均衡，它是指在给定对手策略下，每个玩家都不愿意偏离的策略组合。

纯策略是纳什均衡的一种特殊情况，而混合策略则更为复杂，它允许玩家以概率分布的形式选择行动。

例如，如果一个博弈矩阵中，玩家1混合策略中选择T的概率为0.4，选择B的概率为0.6，这就增加了博弈的不可预测性。

混合策略的引入，使得策略不再是单一的选择，而是概率与策略的巧妙结合。

混合策略纳什均衡的计算涉及到预期收益的分析。

玩家1的策略概要中，每个行动与对应收益的组合形成一个混合策略写法，如q1-qLRpTuTLuTR1-pBuBLuBR。

要找到均衡，每个玩家的混合策略必须满足收益最大化，且相互制约，如硬币问题中，(0.5,0.5)是唯一的纳什均衡，尽管双方都随机选择，但收益为零，形成动态平衡。

双寡头博弈中的应用</

博弈论在经济学中有着广泛应用，如古诺模型和伯特兰模型。

在古诺双寡头模型中，两家公司选择产出，价格由总和决定。

当公司的成本条件满足a>c时，纳什均衡的产量和价格展现出竞争、垄断和寡头市场的区别。

而在伯特兰模型中，价格和产量的关系更为复杂，但每个公司寻求利润最大化的纯策略纳什均衡点(c,c)揭示了市场动态。

在药检博弈中，纳什均衡随着概率的引入发生变化。

尽管检测频率增加，但药检的实际效果并未提升，这说明纳什均衡在复杂情境下可能并非总是最优。

让我们来看一些具体的例子，如例0201的多选题答案AB，以及例0202懦夫博弈中的收益-0.875。

混合策略的数学探索</

混合策略纳什均衡的寻找，有时需要通过代数方法来求解，如例0203中的概率计算和例0204中古诺模型的价格。

在实际问题中，如例0206的药检模型，正确选项C揭示了策略选择的关键特性。

而在卡特尔博弈中，玩家1的收益和p值紧密相关，如例0209所示。

污水排放博弈和募捐博弈展示了纯策略和混合策略纳什均衡的不同类型。在污水排放中，(T;T;D)等纯策略组合代表了污染问题的潜在风险，而募捐博弈中，均衡策略的帕累托最优特性表明了社会合作的微妙平衡。

博弈论的世界充满了无限可能，从纯策略到混合策略，从寡头博弈到复杂的社会互动，每一层深入都揭示出人类决策的智慧与复杂性。

让我们继续在MrFigurant的引导下，探索博弈论的更多奥秘，如在《博弈论03：完全信息扩展式博弈》中深入理解。

(完)