1、极惯性矩的定义就是Ip=∫ρ^2dA,即面积对截面形心取矩的平方再积分。对于圆截面来说,极惯性矩和抗扭惯性矩是一回事,可以等价。
2、但是对于矩形截面轴来说,我们为了套用圆截面轴的扭转变形公式φ=TL/GIp,人为定义了一个矩形截面的抗扭惯性矩It。这样一来,矩形截面轴扭转的扭转角φ=TL/GIt。
It是一个人为定义的物理量,为了具有和极惯性矩一样的量纲,并且把矩形的高和宽反应进来,我们人为定义其计算公式为It=βhb^3,h是矩形的高,b是宽,β是系数,必须根据矩形长宽比来确定,其值从任何一本材料力学教材的表格都可以查到。
3、相对的,对于矩形截面轴,极惯性矩虽然还是Ip=∫ρ^2dA在矩形截面里积分。
但是因为这个量在扭转时用不着,基本上都是不讨论不用的。
非圆(或圆环)截面,一般都是用抗扭惯性矩,而不是用极惯性矩。
例如,箱型梁,开口圆环截面量,工字截面梁等等。
惯性矩计算:
1、截面系数
根据材料力学,在承受弯矩Μ的梁截面上和承受扭矩T的杆截面上,最大的弯曲应力σ和最大的扭转应力τ出现于离弯曲中性轴线和扭转中性点垂直距离最远的面或点上。
σ和τ的数值为-0.032√(C+W)-0.21√(RD↑2)式中Jxx和J0分别为围绕中性轴线XX和中性点O的截面惯性矩;Jxx/y和J0/y分别为弯曲和扭转的截面模量。
一般截面系数的符号为W,单位为毫米3。
依据公式可知,截面的抗弯和抗扭强度与相应的截面系数成正比。
2、回转半径
物理上认为,刚体按一定规律分布的质量,在转动中等效于集中在某一点上的一个质点的质量,此点离某轴线的垂距为k,因此,刚体对某一轴线的转动惯量与该等效质点对此同一轴线的转动惯量相等,即I=mk2.则k称为对该轴线的回转半径。
回转半径的大小与截面的形心轴有关。
最小回转半径一般指非对称截面中(如不等边角钢),对两个形心轴的回转半径中的较小者。
这在计算构件的长细比时,如构件的平面内和平面外计算长度相等时,它的长细比就要用最小回转半径计算。
极惯性矩和惯性矩的区别?
探讨惯性矩、极惯性矩与静矩
在材料力学的领域中,当我们面对“惯性矩”、“极惯性矩”与“静矩”这些术语时,可能觉得它们既抽象又复杂。让我们尝试以一种更直观的方式来理解这三个概念,通过它们在弯曲问题中的应用与意义。
首先,让我们从“惯性矩”谈起。
在弯曲问题中,我们如何解释“惯性矩”的概念?想象一个横截面从直立状态到弯曲状态的变化。
在这一过程中,需要克服的是“惯性矩”——即弯曲过程中产生的力矩。
我们可以通过已知的最大应力、转动半径以及角速度来计算这个力矩,进而理解如何在给定条件下弯曲横截面。
这个解释体现了“惯性矩”的实际应用与物理含义,即在弯曲过程中克服的力矩。
接着,转向“极惯性矩”。
在理解极惯性矩时,我们可以将其视为物体在圆周运动时惯性力产生的矩。
这一概念与“惯性矩”紧密相连,因为它们都关注于旋转运动中力矩的作用。
将这个概念应用到梁的弯曲问题中,即通过计算克服的惯性力矩来理解梁在弯曲过程中所需的力量,体现了“极惯性矩”在力学中的重要作用。
接下来,我们来看看“静矩”。
在解释“静矩”的概念时,我们可以将其理解为静力绕某轴产生的矩。
这一解释强调了静矩在力学中的作用,即在静止状态下力矩的表现形式。
通过计算静矩,我们可以更好地理解静力作用下物体的稳定性与平衡状态。
通过上述解释,我们可以发现“惯性矩”、“极惯性矩”与“静矩”在材料力学中扮演着重要角色。
它们不仅与弯曲问题紧密相关,还与旋转运动及静止状态下的力学分析密切相关。
在理解这些概念时,结合具体实例与物理现象,可以帮助我们更直观地把握它们的物理意义与应用。



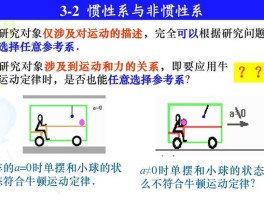




还没有评论,来说两句吧...