离心力是什么意思视频

离心泵引就是根据离心力原理设计的，高速旋转的叶轮叶片带动水转动，将水甩出,从而达到输送的目的。离心泵有好多种，从使用上可以分为民用与工业用泵；从输送介质上可以分为清水泵、杂质泵、耐腐蚀泵等。

离心泵基本构造

离心泵的基本构造是由六部分组成的，分别是：叶轮，泵体，泵轴，轴承，密封环，填料函。

1、叶轮是离心泵的核心部分，它转速高输出力大，叶轮上的叶片又起到主要作用，叶轮在装配前要通过静平衡实验。

叶轮上的内外表面要求光滑，以减少水流的摩擦损失。

2、泵体也称泵壳，它是水泵的主体。

起到支撑固定作用，并与安装轴承的托架相连接。

3、泵轴的作用是借联轴器和电动机相连接，将电动机的转矩传给叶轮，所以它是传递机械能的主要部件。

4、轴承是套在泵轴上支撑泵轴的构件，有滚动轴承和滑动轴承两种。

滚动轴承使用牛油作为润滑剂加油要适当一般为2/3～3/4的体积太多会发热，太少又有响声并发热！滑动轴承使用的是透明油作润滑剂的,加油到油位线。

太多油要沿泵轴渗出并且漂失，太少轴承又要过热烧坏造成事故！在水泵运行过程中轴承的温度最高在85℃一般运行在60度左右，如果高了就要查找原因（是否有杂质，油质是否发黑，是否进水）并及时处理！5、密封环又称减漏环。

叶轮进口与泵壳间的间隙过大会造成泵内高压区的水经此间隙流向低压区，影响泵的出水量，效率降低！间隙过小会造成叶轮与泵壳摩擦产生磨损。

为了增加回流阻力减少内漏，延缓叶轮和泵壳的所使用寿命，在泵壳内缘和叶轮外援结合处装有密封环，密封的间隙保持在0.25～1.10mm之间为宜。

6、填料函主要由填料，水封环，填料筒，填料压盖，水封管组成。

填料函的作用主要是为了封闭泵壳与泵轴之间的空隙，不让泵内的水流流到外面来也不让外面的空气进入到泵内。

始终保持水泵内的真空！当泵轴与填料摩擦产生热量就要靠水封管注水到水封圈内使填料冷却！保持水泵的正常运行。

所以在水泵的运行巡回检查过程中对填料函的检查是特别要注意！在运行600个小时左右就要对填料进行更换。

7、轴向力平衡装置在离心泵运行过程中，由于液体是在低压下进入叶轮，而在高压下流出，使叶轮两侧所受压力不等，产生了指向入口方向的轴向推力，会引起转子发生轴向窜动，产生磨损和振动，因此应设置轴向推力轴承，以便平衡轴向力。

离心力是什么术语

在第1-3课“为什么选择椭圆？”村山教授使用术语“离心力”，这可能会使许多被告知离心力是虚构且不存在的学生感到困惑。

从技术上讲，村山教授是正确的，但他的演讲需要更高级的物理学知识，我们可以在不使用离心力的情况下充分解释相同的现象。

非常简单（后面会给出更长的解释），村山教授正在考虑一个所谓的非惯性参考系，其中存在虚构的离心力。

但是，我们可以在惯性系中很好地评估问题，并利用向心力，这是一种真实的力。

这种分析可能是接触过一些物理的学生最熟悉的。

使用向心力的解释：考虑一个围绕太阳运行圆形轨道的行星。如果我们想象在图表上画出这条轨道，我们会将太阳置于x-y轴的原点，行星将在xy平面上围绕太阳做一个圆圈。重力是。

在上面，负号表示力的方向。

特别是，由于太阳产生的地球上的力总是指向太阳。

准确地说，我们应该使用向量来恰当地描述这一点，，其中表示力点径向向内。

如果您还没有接触过矢量，请不要担心；他们在这个问题中解决的唯一问题与减号有关，我们总是可以使用物理直觉来确保答案的符号是正确的。

圆形轨道上的行星正在加速。当然，这种加速度是由于重力。圆形运动的物体具有指向圆心的加速度，由下式给出，在矢量记号中为。

这就是所谓的向心加速度。使用牛顿定律F=ma（向量：）我们知道万有引力导致加速度。

现在我们可以求解速度并得出与村山教授在讲座中得到的相同答案：

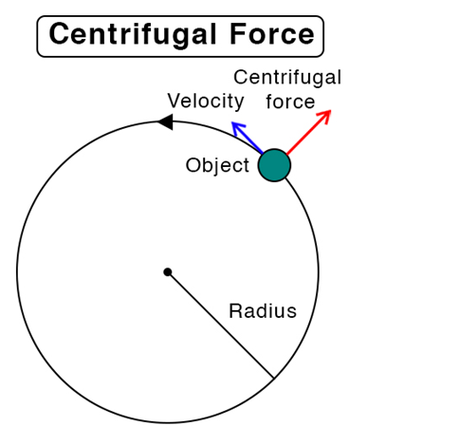
使用离心力的解释：想象你的双腿被一根绳子绑在一起，某个巨人在你头顶上绕了一圈。

你感觉好像你被向外拉，即有一个力向外指向，远离轨道中心。

这就是所谓的离心力。

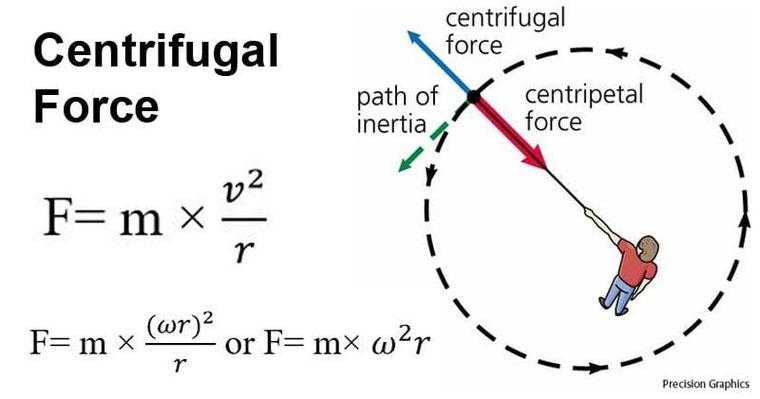
离心力不是真正的力；对你在地上看着巨人旋转你的朋友来说，他们只识别巨人拉绳子的向心力。

这种向心力指向围绕巨人头部的轨道中心。

好吧，你坚持绕着巨大的脑袋旋转，离心力是不真实的，但是你很能感觉到被拉向外的痛苦。解决方案是您坚持在所谓的非惯性框架中测量力（你的感受）。

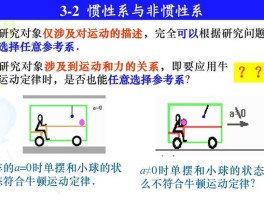
非惯性系是一组正在加速的坐标（它既不是静止的也不是匀速的）。对于自己正在加速的人来说，这是一组自然的坐标，因为相对于他们自己的运动，坐标总是静止的。

继续使用你被旋转的类比可能会让人感到困惑，所以让我们切换回绕太阳运行的行星。

对于此示例，将一组坐标附加到随行星移动的行星。

这是一个非惯性系，因为坐标本身在圆周运动中被加速。

让我们将非惯性系内的加速度表示为a'。

在这些坐标中，行星没有加速，a'=0。

引力将行星拉向一个方向。

根据牛顿定律，在非惯性系内，必须有其他力抵消万有引力，使a'=0。

这就是虚构的离心力。

在方程中，应用牛顿定律ma'=ΣF和a'=0我们有：ma'=0=ΣF=F引力+F离心力

在非惯性系中，我们可以取引力指向负方向，，然后离心力指向相反方向，。将离心力移到等式的另一边有。

现在我们可以求解速度并得出与以前相同的答案。

总而言之，在非惯性坐标系中——坐标加速并“附着”到行星上——我们必须引入离心力以确保非惯性坐标系中的加速度为零。

这就是当你转身时你感觉到向外拉的力量的来源。

虽然这种分析是完全有效的，但在保持固定的惯性框架中评估问题要容易得多。

这个惯性系有固定的坐标，行星在这些坐标内运动。

我们在这些笔记的开头使用了这样的惯性系。