向量的运算的所有公式(向量的运算的所有公式图片)

向量a=x1，y1，向量b=x2，y2，a·b=x1x2+y1y2=abcosθθ是a，b夹角，向量之间不叫quot乘积quot，而叫数量积，如a·b叫做a与b的数量积或a点乘b已知两个非零向量ab，那么a·b=abcosθ。

向量的运算的所有公式是1加法已知向量ABBC，再作向量AC，则向量AC叫做ABBC的和，记作AB+BC，即有AB+BC=AC2减法ABAC=CB，这种计算法则叫做向量减法的三角形法则，简记为共起点连中点指被减。

1单位向量单位向量a0=向量a向量a2Px，y那么向量OP=x向量i+y向量j向量OP=根号x平方+y平方3P1x1，y1P2x2，y2那么向量P1P2=｛x2x1，y2y1｝向量P1P2=根号x2x1平方+y2。

1向量的加法向量加法的运算律交换律a+b=b+a结合律a+b+c=a+b+c2向量的减法如果ab是互为相反的向量，那么a=b，b=a，a+b=00的反向量为0ABAC=CB即“共同起点，指向被减”。

OP=OP1+λOP21+λ定比分点向量公式x=x1+λx21+λ，y=y1+λy21+λ定比分点坐标公式我们把上面的式子叫做有向线段P1P2的定比分点公式三点共线定理若OC=λOA+μOB，且λ。

如下1向量的加法向量的加法满足平行四边形法则与三角形法则AB+BC=ACa+b=x+x#39，y+y#39a+0=0+a=a向量加法的运算律交换律a+b=b+a结合律a+b+c=a+b+c2向量的减法如果a。

1向量的加法向量加法的运算律交换律a+b=b+a结合律a+b+c=a+b+c2向量的减法如果ab是互为相反的向量，那么a=b，b=a，a+b=00的反向量为0ABAC=CB即“共同起点，指向。

交换律a+b=b+a结合律a+b+c=a+b+c在数学中，向量也称为欧几里得向量几何向量矢量，指具有大小magnitude和方向的量它可以形象化地表示为带箭头的线段箭头所指代表向量的方向线段长度。

加法减法和数乘1加法已知向量ABBC，再作向量AC，则向量AC叫做ABBC的和，记作AB+BC，即有AB+BC=AC2减法ABAC=CB，这种计算法则叫做向量减法的三角形法则，简记为共起点连中点指被减3数。

1设a=x，y，b=x，y向量的加法向量加法的运算律交换律a+b=b+a结合律a+b+c=a+b+c2向量的减法如果ab是互为相反的向量，那么a=b，b=a，a+b=00的反向量为0ABAC=CB。

a=x，y，b=x#39，y#391向量的加法向量的加法满足平行四边形法则和三角形法则AB+BC=ACa+b=x+x#39，y+y#39a+0=0+a=a向量加法的运算律交换律a+b=b+a结合律a+b+c=a+b+c2向量的。

#160#160#160#160#160#160OP=OP1+λOP21+λ定比分点向量公式#160#160#160#160#160#160x=x1+λx21+λ，#160#160#160#160#160#160y。

向量积公式向量积c=a×b=absin向量相乘分内积和外积内积ab=，ab，cosα内积无方向，叫点乘外积a×b=，ab，sinα外积有方向，叫×乘那个读差，即差乘，方便表达所以用差另外。

空间向量公式D=AS*BQ如果三个向量abc不共面，那么对空间任一向量p，存在一个唯一的有序实数组x，y，z，使p=xa+yb+zc任意不共面的三个向量都可作为空间的一个基底，零向量的表示唯一本文由101教育。

单位向量a0=向量a向量a1如果x#178+y#178+z#178=1，则向量x，y，z称为单位向量2只要模为1的向量，就称为单位向量，单位向量有无穷多个，在任何一个方向上都有一个单位向量3单位向量是指。

向量积公式如下向量积c=a×b=absin向量相乘分内积和外积内积ab=，ab，cosα内积无方向，叫点乘外积a×b=，ab，sinα外积有方向，叫×乘那个读差，即差乘，方便表达所以用。

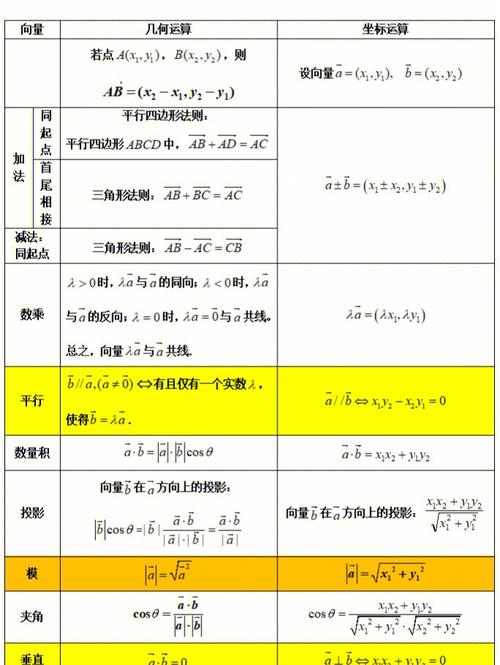
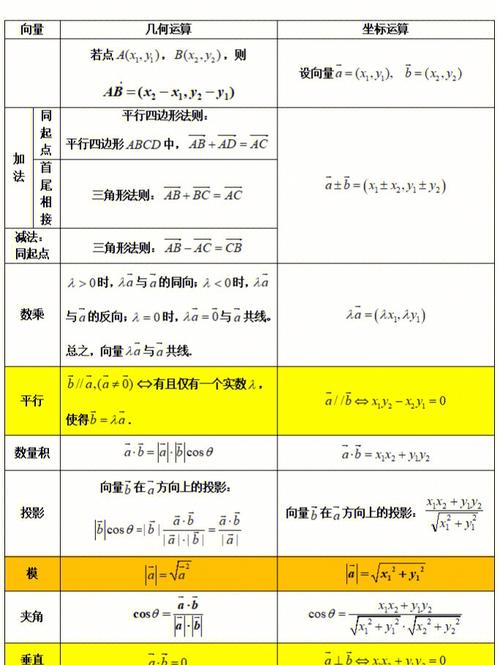
向量的运算的所有公式图片

分析如下:

向量的叉乘公式:

(x1,y1,z1)X(x2,y2,z2)=(y1z2-y2z1,z1x2-z2y1,x1y2-x2y1)。

因为直角坐标系下，a=a1i+a2j+a3k,b=b1i+b2j+b3k;而i=j×k，j=k×i，k=i×j（右手系），且。

i×i=0，j×j=0，k×k=0，再利用叉乘的分配律推算一下。

拉格朗日公式这是一个著名的公式,而且非常有用：a×(b×c)=b（a·c）−c（a·b）。

向量叉乘的分配律的证明:

ax(b+c)=axb+axc?

这个可以用向量a，b，c的座标带进去，订边右边分别计算出结果，并证明相等。

向量叉乘公式是什么,

叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量为c。

|向量c|=|向量a×向量b|=|a||b|sin。

向量c的方向与a,b所在的平面垂直，且方向要用“右手法则”判断（用右手的四指先表示向量a的方。

向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向）。

因此向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a,。

在物理学中，已知力与力臂求力矩，就是向量的外积，即叉乘。

将向量用坐标表示（三维向量），若向量a=(a1,b1,c1)，向量b=(a2,b2,c2)，。

则向量a×向量b=

|ijk|

|a1b1c1|

|a2b2c2|

=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)。

（i、j、k分别为空间中相互垂直的三条坐标轴的单位向量）。

拓展资料

1、如下图利用加减消元法，为了容易记住其求解公式，但要记住这个求解公式是很困难的，因此引入三阶行列式的概念。记称左式的左边为三阶行列式，右边的式子为三阶行列式的展开式。

2、计算方法:

a、直接计算——对角线法,标准方法是在已给行列式的右边添加已给行列式的第一列、第二列。

我们把行列式的左上角到右下角的对角线称为主对角线，把右上角到左下角的对角线称为次对角线。

这时，三阶行列式的值等于主对角线的三个数的积与和主对角线平行的三个对角线上的数的积的和减去次对角线的三个数的积与和次对角线平行的对角线上三个数的积的和的差。

b、任何一行或一列展开——代数余子式,行列式某元素的余子式：行列式划去该元素所在的行与列的各元素,剩下的元素按原样排列,得到的新行列式。

行列式某元素的代数余子式：行列式某元素的余子式与该元素对应的正负符号的乘积.即行列式可以按某一行或某一列展开成元素与其对应的代数余子式的乘积之和。

3、性质:

a、行列式与它的转置行列式相等。

b、互换行列式的两行(列)，行列式变号。

c、如果行列式有两行(列)完全相同，则此行列式为零。

d、行列式的某一行(列)中所有的元素都乘以同一数k，等于用数k乘此行列式。

e、行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。

f、行列式中如果有两行(列)元素成比例，则此行列式等于零。

g、把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变。