什么是惯性参考系的定义

对一切运动的描述，都是相对于某个参考系的。

参考系选取的不同，对运动的描述，或者说运动方程的形式，也随之不同。

在有些参考系中，不受力的物体会保持相对静止或匀速直线运动状态，其时间是均匀流逝的，空间是均匀和各向同性的。

在这样的参考系内，描述运动的方程有着最简单的形式，此参考系就是惯性参考系（惯性系）。

朗道《场论》（主要是相对论电动力学）给出的定义：牛顿第一定律成立的参照系叫做惯性系（原文直接说在这样的参考系中，一个不受相互作用的粒子将保持相对静止或匀速直线运动）。

这个定义在牛顿力学和狭义相对论中均适用。

①牛顿第一定律定义了惯性系。

②牛顿力学在惯性系中成立（在相对论中，修正为麦克斯韦方程组和相对论力学在其中成立）。

这样就不存在逻辑循环，同时也说明，牛顿第一定律不是牛顿第二定律在F=0时的特殊情况。

在空间中，相对于任何参考点（静止中或移动中），一个运动中的粒子的位移、速度和加速度都可以测量计算而求得。

虽然如此，经典力学假定有一组特别的参考系。

在这组特别的参考系内，大自然的力学定律呈现出比较简易的形式，称这些特别的参考系为惯性参考系（惯性系）。

惯性系有个特性：两个惯性系之间的相对速度必是常数；相对于一个惯性系，任何非惯性参考系（非惯性系）必定呈加速度运动。

所以，一个净外力是零的点粒子在任何惯性参考系内测量出的速度必定是常数；只有在净外力非零的状况下，才会有点粒子加速度运动。

因为万有引力的存在，并无任何方法能够保证找到净外力为零的惯性系。

实际而言，相对于遥远星体呈现常速度运动的参考系应是优良的选择。

惯性系是不存在引力作用、不存在自身加速度的“自由”参考系。

在经典力学中，这是一种理想参考系：由于宇宙空间中无处不存在引力，实际的惯性系是不存在的。

在广义相对论中，由于引力作用和加速度是完全等效的，对于一个在引力场中作自由落体运动的参考系，引力作用和自身加速度的作用抵消。

这样的参考系，是一个真实的“自由”参考系。

由于引力场在空间中的分布是不均匀的，惯性系只可能是局域的，也被称为局域惯性参考系。

宇宙中不存在全局惯性参考系。

什么是惯性参考系的定义和特点

牛顿力学的基石之一——惯性参照系，其实并非牛顿的原创，而是1885年由德国物理学家揭示的概念。

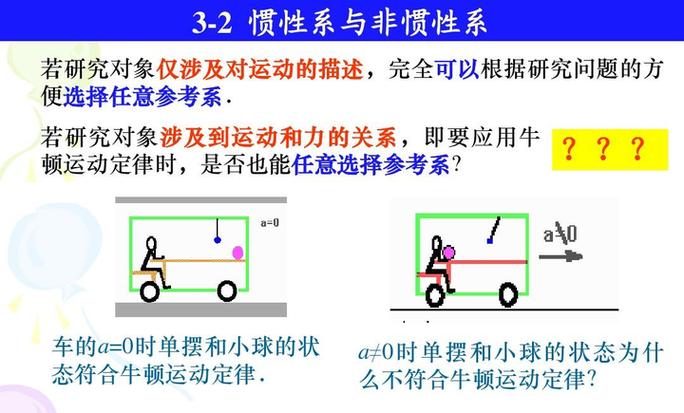
尽管常与牛顿的名字关联，但它是基于牛顿运动定律成立的特殊参考系，其中加速度为零<a=0，确保定律的有效性。

所有惯性系具有一个关键特性：它们之间是等效的，这意味着在任何两个惯性系中，物理定律的表现形式是相同的。要判断一个参考系是否为惯性系，唯一的标准是通过实验验证牛顿定律是否适用，这是最根本的判据。

伽利略相对性原理进一步扩展了我们对惯性系的理解，任何与惯性参照系保持静止或匀速直线运动的状态也是惯性系。

在实际应用中，人们根据问题的特性来选择最接近真实的惯性参考系。

例如，研究地表附近物体运动时，地球坐标系作为一个近似的惯性系，对于工程技术问题非常实用。

在探讨太阳系的天体运动时，太阳则成为另一个理想的惯性参照系。每个具体情境下，我们都会根据实际需求，选择最符合的惯性系来简化复杂的物理问题分析。

总的来说，惯性参照系是科学研究中的重要工具，它在物理世界中起着至关重要的作用。通过实验验证和实际应用，我们得以在日常生活中理解和运用这些概念。希望这段分享能帮助你深化对惯性参照系的理解。