离心力是什么意思简单说明(离心力是什么术语)

离心力是一种虚拟力，是一种惯性力，以下将惯性离心力和离心力概念简单解释一下：

我们通常是以地面做参考系，可设想地面是静止的，或者在不太长的距离中把地面运动视为匀速直线运动，即惯性参考系，牛顿就是在这样的前提下才总结出了运动定律。

如果参考系是变速的，即非惯性参考系，牛顿定律就不能直接应用了，因此人们假想出了“惯性”来解决牛顿定律的应用问题。

惯性离心力是非惯性系中的假想力。

下面举匀速圆周运动例子：

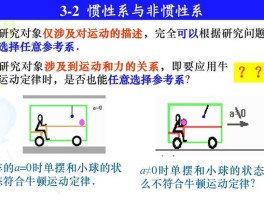
匀速圆周运动的线速度方向时刻变化，说明有向心加速度，而向心加速度方向也时刻变化，这是个典型的非惯性系。

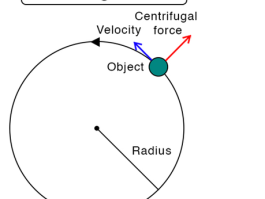
如果有个大转盘在作匀速圆周运动，你坐到盘上不要看周围景物，此时就把自己置身于非惯性系了，你肯定会感觉到有某种力量想把自己推下来，而此时又没有任何施力物推你，这种力量就称为惯性离心力。

最后提醒一点，所谓"惯性力"只存在于非惯性系，是一种虚拟力，是为了将牛顿定律推广到非惯性系上使用而虚拟的一种力，在加上这样的虚拟力后除了牛顿第三定律外，牛顿力学中的各种定律、定理在非惯性系上都可以得以运用。

离心力是什么术语

改写后的文本：

行星绕太阳做匀速圆周运动的向心力由万有引力提供，根据牛顿第二定律，该向心力可表示为F=mv^2/r，其中m为行星质量，v为行星速度，r为行星到太阳的距离。

同样，使用角速度ω描述运动时，向心力也可以表示为F=mω^2r。

地球的第一宇宙速度是指在地球表面附近绕地球做匀速圆周运动的人造卫星的运行速度。

轨道半径相当于地球半径R，此时万有引力提供了卫星做圆周运动的向心力。

根据牛顿第二定律和万有引力定律，我们有mg=mv^2/R，从而解得第一宇宙速度v=sqrt(gR)，其中g为地球表面的重力加速度，取值为10m/s^2，R为地球半径，约为6.4×10^6m。

计算得到地球的第一宇宙速度大约为7.9km/s。

离心力并不存在，正确的术语应该是有向心力。

向心力是指物体在做圆周运动时向圆心的力，其大小可由F=mv^2/r或F=mω^2r计算得出，其中m是物体的有效质量，v是线速度，r是圆周运动的半径，ω是角速度。

向心力的大小取决于物体的质量、速度以及圆周运动的半径。

相对离心力Fcf通常用来表示向心力与地球引力G的比值，其计算公式为Fcf=1.119×10^5(h)^2r/g，其中h是离心半径（单位为cm），g是地球表面的重力加速度。