1孕育阶段
这个阶段主要是指1956年以前。自古以来,人们就一直试图用各种机器来代替人的部分脑力劳动,以提高人们征服自然的能力,其中对人工智能的产生、发展有重大影响的主要研究成果包括:
早在公元前384-公元前322年,伟大的哲学家亚里士多德(Aristotle)就在他的名著《工具论》中提出了形式逻辑的一些主要定律,他提出的三段论至今仍是演绎推理的基本依据。
英国哲学家培根(F.Bacon)曾系统地提出了归纳法,还提出了“知识就是力量”的警句。这对于研究人类的思维过程,以及自20世纪70年代人工智能转向以知识为中心的研究都产生了重要影响。
德国数学家和哲学家莱布尼茨(G.W.Leibniz)提出了万能符号和推理计算的思想,他认为可以建立一种通用的符号语言以及在此符号语言上进行推理的演算。
这一思想不仅为数理逻辑的产生和发展奠定了基础,而且是现代机器思维设计思想的萌芽。
英国逻辑学家布尔(C.Boole)致力于使思维规律形式化和实现机械化,并创立了布尔代数。他在《思维法则》一书中首次用符号语言描述了思维活动的基本推理法则。
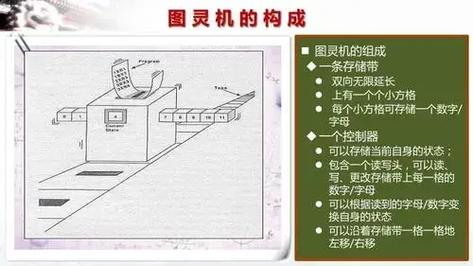
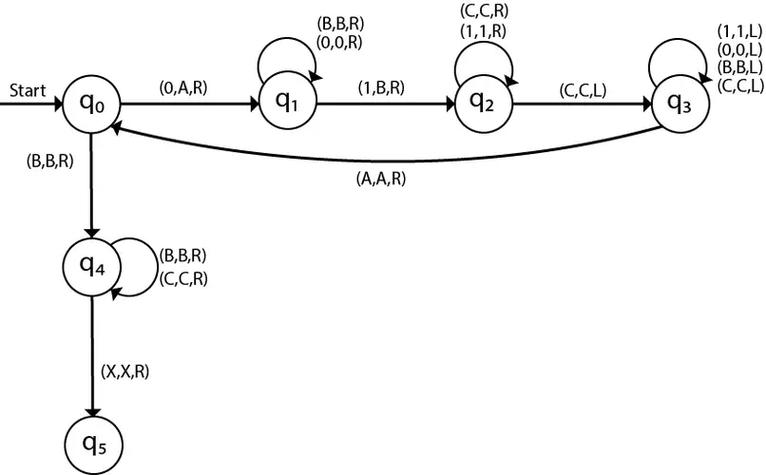
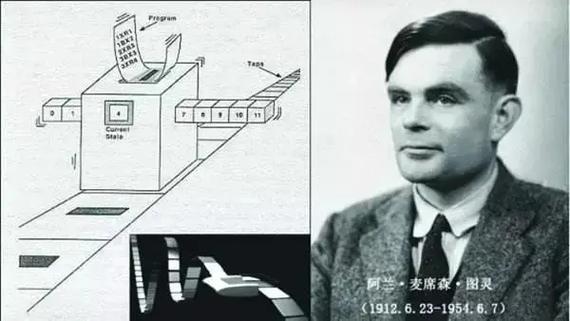
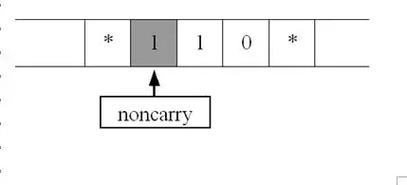
英国数学家图灵(A.M.Turing)在1936年提出了一种理想计算机的数学模型,即图灵机,为后来电子数字计算机的问世奠定了理论基础。
美国神经生理学家麦克洛奇(W.McCulloch)与匹兹(W.Pitts)在1943年建成了第一个神经网络模型(M-P模型),开创了微观人工智能的研究领域,为后来人工神经网络的研究奠定了基础。
美国爱荷华州立大学的阿塔纳索夫(Atanasoff)教授和他的研究生贝瑞(Berry)在1937年至1941年间开发的世界上第一台电子计算机“阿塔纳索夫-贝瑞计算机(Atanasoff-BerryComputer,ABC)”为人工智能的研究奠定了物质基础。
需要说明的是:世界上第一台计算机不是许多书上所说的由美国的莫克利和埃柯特在1946年发明。
这是美国历史上一桩著名的公案。
这个阶段主要是指1970年以后。
进入20世纪70年代,许多国家都开展了人工智能的研究,涌现了大量的研究成果。
例如,1972年法国马赛大学的科麦瑞尔(A.Comerauer)提出并实现了逻辑程序设计语言PROLOG;斯坦福大学的肖特利夫(E.H.Shorliffe)等人从1972年开始研制用于诊断和治疗感染性疾病的专家系统MYCIN。
但是,和其他新兴学科的发展一样,人工智能的发展道路也不是平坦的。
例如,机器翻译的研究没有像人们最初想象的那么容易。
当时人们总以为只要一部双向词典及一些词法知识就可以实现两种语言文字间的互译。
后来发现机器翻译远非这么简单。
实际上,由机器翻译出来的文字有时会出现十分荒谬的错误。
例如,当把“眼不见,心不烦”的英语句子“Outofsight,outofmind”。
翻译成俄语变成“又瞎又疯”;当把“心有余而力不足”的英语句子“Thespiritiswillingbutthefleshisweak”翻译成俄语,然后再翻译回来时竟变成了“Thewineisgoodbutthemeatisspoiled”,即“酒是好的,但肉变质了”;当把“光阴似箭”的英语句子“Timeflieslikeanarrow”翻译成日语,然后再翻译回来的时候,竟变成了“苍蝇喜欢箭”。
由于机器翻译出现的这些问题,1960年美国政府顾问委员会的一份报告裁定:“还不存在通用的科学文本机器翻译,也没有很近的实现前景。
”因此,英国、美国当时中断了对大部分机器翻译项目的资助。
在其他方面,如问题求解、神经网络、机器学习等,也都遇到了困难,使人工智能的研究一时陷入了困境。
人工智能研究的先驱者们认真反思,总结前一段研究的经验和教训。
1977年费根鲍姆在第五届国际人工智能联合会议上提出了“知识工程”的概念,对以知识为基础的智能系统的研究与建造起到了重要的作用。
大多数人接受了费根鲍姆关于以知识为中心展开人工智能研究的观点。
从此,人工智能的研究又迎来了蓬勃发展的以知识为中心的新时期。
这个时期中,专家系统的研究在多种领域中取得了重大突破,各种不同功能、不同类型的专家系统如雨后春笋般地建立起来,产生了巨大的经济效益及社会效益。
例如,地矿勘探专家系统PROSPECTOR拥有15种矿藏知识,能根据岩石标本及地质勘探数据对矿藏资源进行估计和预测,能对矿床分布、储藏量、品位及开采价值进行推断,制定合理的开采方案。
应用该系统成功地找到了超亿美元的钼矿。
专家系统MYCIN能识别51种病菌,正确地处理23种抗菌素,可协助医生诊断、治疗细菌感染性血液病,为患者提供最佳处方。
举例:
①教书的来了(“教书的”是转指,转指教书的“人”);教书的时候要认真(“教书的”语义没变,是自指)。
②Unplug一词的原意为“不使用(电源)插座”,是自指;常用来转指为不使用电子乐器的唱歌。
③colored在表示havingcolour(着色)时是自指。colored在表示有色人种时,就是转指。
④rich,富有的,是自指。therich,富人,是转指。
知识本身也是一个概念。据此,人工智能的问题就变成了如下三个问题:一、如何定义(或者表示)一个概念、如何学习一个概念、如何应用一个概念。因此对概念进行深人研究就非常必要了。
那么,如何定义一个概念呢?简单起见,这里先讨论最为简单的经典概念。
经典概念的定义由三部分组成:第一部分是概念的符号表示,即概念的名称,说明这个概念叫什么,简称概念名;第二部分是概念的内涵表示,由命题来表示,命题就是能判断真假的陈述句。
第三部分是概念的外延表示,由经典集合来表示,用来说明与概念对应的实际对象是哪些。
举一个常见经典概念的例子——素数(primenumber),其内涵表示是一个命题,即只能够被1和自身整除的自然数。
概念有什么作用呢?或者说概念定义的各个组成部分有什么作用呢?经典概念定义的三部分各有作用,且彼此不能互相代替。具体来说,概念有三个作用或功能,要掌握一个概念,必须清楚其三个功能。
第一个功能是概念的指物功能,即指向客观世界的对象,表示客观世界的对象的可观测性。
对象的可观测性是指对象对于人或者仪器的知觉感知特性,不依赖于人的主观感受。
举一个《阿Q正传》里的例子:那赵家的狗,何以看我两眼呢?句子中“赵家的狗”应该是指现实世界当中的一条真正的狗。
但概念的指物功能有时不一定能够实现,有些概念其设想存在的对象在现实世界并不存在,例如“鬼”。
第二个功能是指心功能,即指向人心智世界里的对象,代表心智世界里的对象表示。
鲁迅有一篇著名的文章《论丧家的资本家的乏走狗》,显然,这个“狗”不是现实世界的狗,只是他心智世界中的狗,即心里的狗(在客观世界,梁实秋先生显然无论如何不是狗)。
概念的指心功能一定存在。
如果对于某一个人,一个概念的指心功能没有实现,则该词对于该人不可见,简单地说,该人不理解该概念。
最后一个功能是指名功能,即指向认知世界或者符号世界表示对象的符号名称,这些符号名称组成各种语言。
最著名的例子是乔姆斯基的“colorlessgreenideassleepfuriously”,这句话翻译过来是“无色的绿色思想在狂怒地休息”。
这句话没有什么意思,但是完全符合语法,纯粹是在语义符号世界里,即仅仅指向符号世界而已。
当然也有另外,“鸳鸯两字怎生书”指的就是“鸳鸯”这两个字组成的名字。
一般情形下,概念的指名功能依赖于不同的语言系统或者符号系统,由人类所创造,属于认知世界。
同一个概念在不同的符号系统里,概念名不一定相同,如汉语称“雨”,英语称“rain”。
根据波普尔的三个世界理论,认知世界、物理世界与心理世界虽然相关,但各不相同。
因此,一个概念的三个功能虽然彼此相关,也各不相同。
更重要的是,人类文明发展至今,这三个功能不断发展,彼此都越来越复杂,但概念的三个功能并没有改变。
在现实生活中,如果你要了解一个概念,就需要知道这个概念的三个功能:要知道概念的名字,也要知道概念所指的对象(可能是物理世界)。
更要在自己的心智世界里具有该概念的形象(或者图像)。
如果只有一个,那是不行的。
知道了概念的三个功能之后,就可以理解人工智能的三个学派以及各学派之间的关系。
人工智能也是一个概念,而要使一个概念成为现实,自然要实现概念的三个功能。
人工智能的三个学派关注于如何才能让机器具有人工智能,并根据概念的不同功能给出了不同的研究路线。
专注于实现AI指名功能的人工智能学派成为符号主义,专注于实现AI指心功能的人工智能学派称为连接主义,专注于实现AI指物功能的人工智能学派成为行为主义。
1.符号主义
符号主义的代表人物是Simon与Newell,他们提出了物理符号系统假设,即只要在符号计算上实现了相应的功能,那么在现实世界就实现了对应的功能,这是智能的充分必要条件。
因此,符号主义认为,只要在机器上是正确的,现实世界就是正确的。
说得更通俗一点,指名对了,指物自然正确。
在哲学上,关于物理符号系统假设也有一个著名的思想实验——本章1.1.3节中提到的图灵测试。图灵测试要解决的问题就是如何判断一台机器是否具有智能。
图灵测试将智能的表现完全限定在指名功能里。
但马少平教授的故事已经说明,只在指名功能里实现了概念的功能,并不能说明一定实现了概念的指物功能。
实际上,根据指名与指物的不同,哲学家约翰·塞尔勒专门设计了一个思想实验用来批判图灵测试,这就是著名的中文屋实验。
中文屋实验明确说明,即使符号主义成功了,这全是符号的计算跟现实世界也不一定搭界,即完全实现指名功能也不见得具有智能。
这是哲学上对符号主义的一个正式批评,明确指出了按照符号主义实现的人工智能不等同于人的智能。
自动机理论起源于30年代的图灵机概念。
50年代初,J.诺伊曼提出了有自繁殖功能的计算机概念。
王浩在50年代中期提出了一种比原始图灵机更接近现实机器的机器,并证明这种机器与图灵机等价。
60年代,又有人提出了具有随机存取存储器的计算机和多带图灵机。
形式语言理论则源自数理语言学中的乔姆斯基理论,分为四种语言类型,并对应四种形式文法。
2型语言最受关注,与四类自动机之间存在对应关系。
程序设计理论包括程序正确性证明和程序验证。
诺伊曼等人在40年代后期提出借助证明验证程序正确性的方法。
图灵进一步证明了子程序的正确性,其方法是:若程序执行前谓词P成立,则执行后谓词Q成立,程序正确性得证。
这种方法在P.瑙尔和E.F.费洛伊德提出后引起了重视。
J.T.施瓦兹和M.戴维斯在70年代后期提出了一种“正确程序技术”,通过组合数千种基本程序模块和验证方法来确保程序正确性。
循环不变式在程序研究中也有应用。
不同于过去找出循环不变式来证明程序正确性,现在在编程前根据需求找出循环不变式来生成程序。
自动程序设计概念也起源于40年代,图灵提出使用定理证明设计程序。
程序语言的形式语法和形式语义研究在60年代后有了较大发展,但形式语义学尚未完全满足软件技术需求。
程序逻辑在60年代末发展起来,用于程序正确性证明。
算法逻辑和程序逻辑在原有的逻辑基础上增加了程序算子。
算法分析和计算复杂性理论研究算法复杂性,分为算法分析和计算复杂性理论。
计算复杂性理论是可计算性理论的一部分,研究各种递归函数的计算复杂性。
实际可计算性是一个直观但难以精确描述的概念,通常以计算时间多项式有界函数定义。
P=?NP问题关注确定性机器与非确定性机器的解题能力比较。
关于计算和算法的研究,对串行计算性质研究较多,而并行计算性质研究相对不足,特别是异步并行计算。并行计算研究可能成为计算机理论的重要研究方向。
关于计算和计算机械的数学理论,也称为计算理论或计算机科学的数学基础。理论计算机科学主要包括:①自动机论与形式语言理论②程序理论③形式语义学④算法分析和计算复杂性理论











还没有评论,来说两句吧...