层次分析法的基本原理(层次分析法的基本原理是什么)

层次分析法：决策智慧的钥匙

层次分析法，如同一把解锁复杂决策的密钥，诞生于20世纪70年代，由托马斯·塞蒂大师精心打造，旨在将定性与定量相结合，为多目标决策提供有力工具。

无论是经济管理中的策略规划，还是工程领域的优化选择，它都以其系统性与实用性，成为众多领域解决问题的利器。

理解层次，构建模型

决策并非盲目的选择，而是对多种方案进行评估的过程。

比如，选择冰箱、旅游目的地或科研课题，都需要一套清晰的标准。

层次分析法的关键在于分解问题，构建层次结构模型，将目标、准则和备选方案分级，用1-9标度对权重进行客观比较。

判断矩阵的力量

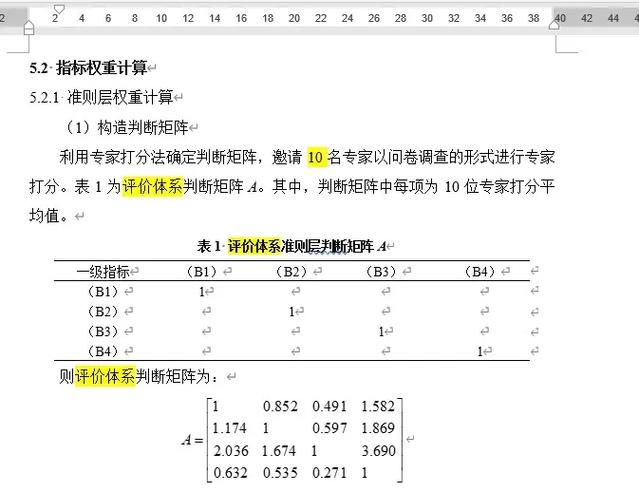
构建的判断矩阵是层次分析的核心。

它是决策者主观判断的量化表达，通过一致性检验，确保权重分配的合理性。

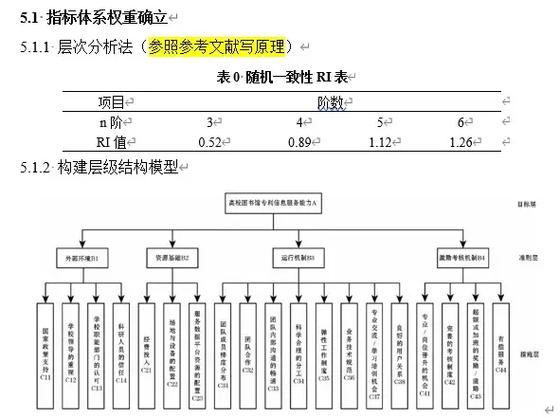
一致性指标CI和随机一致性指标RI，CI接近于零表示理想的一致性，当CR小于0.1，我们可以说分析结果达到了可接受的精度。

通过这个过程，我们得到归一化特征向量，作为权向量，赋予每个要素决策的重要性。

深度解析与实例演示

在旅游选择问题中，我们能看到判断矩阵的构建与一致性检验的细致过程。

通过多层判断矩阵，从上至下，逐步形成总排序。

如果在B层的层次总排序一致性比率CR达标，那么我们就继续向下层进行；否则，就需要调整权重或重新审视结构。

层次分析法的步骤：建模、构造判断矩阵、单排序与总排序一致性检验，环环相扣，展示了其强大的实用性。

优缺点与注意事项

尽管层次分析法能有效处理复杂问题，但它并非万能。

它无法激发新的方案创意，对判断的精细度有一定要求，而且主观性较强。

在应用时，确保要素的合理性、层次结构的准确性和权重计算方法（几何平均法或规范列平均法）的正确选择至关重要。

无论是商品选购、干部选拔，还是其他实际决策，层次分析法都能提供清晰的决策路径。

总结来说，层次分析法是一种强大的决策工具，它以系统性、实用性和简洁性赢得了广泛的认可。通过理解其原理，掌握构造判断矩阵和一致性检验，你将能在面对复杂决策时游刃有余。

层次分析法的基本原理是什么

一、层次分析法与模糊层次分析法的区别主要体现在以下三个方面：

1.基本原理不同：

层次分析法依据问题的性质和目标，将问题分解为不同因素，并按照因素间的关联和隶属关系组成多层次的分析结构模型。其目的是确定最低层（如决策方案）相对于最高层（如总目标）的相对重要权值或优劣次序。

模糊层次分析法则结合了定性和定量分析，使用三角模糊数来量化因素间的比较判断，形成模糊判断矩阵。

2.建立的判断矩阵不同：

层次分析法中的判断矩阵是基于元素的两两比较，旨在建立一致性判断矩阵。

而模糊层次分析法中的判断矩阵则是通过元素的两两比较建立带有模糊性的的一致判断矩阵。

3.权重求解方法不同：

在层次分析法中，检验判断矩阵的一致性通常较为困难，且一致性的标准CR<0.1的科学依据不足，与人类思维的一致性存在差异。

模糊层次分析法则通过使用三角模糊数来定量化因素比较，避免了传统方法的一致性检验问题。

二、模糊层次分析法的应用：

模糊层次分析法（FAHP）改进了传统层次分析法的不足，提高了决策的可靠性。

FAHP有两种主要形式：一种基于模糊数，另一种基于模糊一致性矩阵。

FAHP通过量化评价指标，为选择最优方案提供了依据，并在多个领域得到了广泛应用。

特别是当评价指标较多时，传统的层次分析法难以保证思维的一致性，而FAHP能够有效解决这一问题。