纳什均衡是指这样一种均衡:在这一均衡中,每个博弈参与人都确信,在给定其他参与人战略决定的情况下,他选择了最优战略以回应对手的战略。
”也就是说,所有人的战略都是最优的。
而讲解“纳什均衡”的最著名的案例就是“囚徒的困境”。
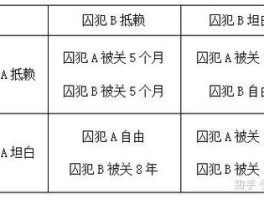
a,b两个囚徒,a坦白b抵赖,b判10年,a判1年.若两人均坦白则各判5年,若两人均抵赖则都判2年。a,b面临抉择。
显然最好的策略是双方都抵赖,结果是大家都只被判2年。
但是由于两人处于隔离的情况下无法串供,按照亚当·斯密的理论,每一个人都是一个“理性的经济人”,都会从利己的目的出发进行选择。
这两个人都会有这样一个盘算过程:假如他招了,我不招,得坐10年监狱,招了才5年,所以招了划算;假如我招了,他也招,得坐5年,他要是不招,我就只坐1年,而他会坐10年牢,也是招了划算。
综合以上几种情况考虑,不管他招不招,对我而言都是招了划算。
两个人都会动这样的脑筋,最终,两个人都选择了招,结果都被判5年刑期。
原本对双方都有利的策略(抵赖)和结局(被判1年刑)就不会出现。这就是著名的“囚徒困境”。它实际上反映了一个很深刻的问题,这就是个人理性与集体理性的矛盾。
对於多人参与、非零和的博弈问题,在纳什之前,无人知道如何求解,或者说怎样找到类似于最小最大解那样的“平衡”。
而找不到解,下面的研究当然无法进行,更谈不上指导实践了。
纳什对博弈论的巨大贡献,正在於他天才性地提出了“纳什均衡”的基本概念,为更加普遍广泛的博弈问题找到了解。
纳什均衡的基本思想是,在这个解集中所有参与者的策略都是对其他参与者所用策略的最佳对策,没有人能够通过单单改变自己的策略提高收益。
求解纳什均衡的方法有哪些
在策略博弈的探索中,我们从纯策略纳什均衡出发,遇到了无法找到纯策略均衡的情况,如石头剪刀布的博弈。
为解决这一问题,引入了混合策略的概念。
混合策略中,玩家选择策略时加入随机性,即在一次博弈中随机地选择一种纯策略。
这种策略的引入,使博弈中没有纯策略的纳什均衡,变为存在混合策略的纳什均衡。
混合策略博弈的数学表示中,每个玩家的策略集构成一个“样本空间”,每种纯策略被赋予一个概率。
定义为在策略集上的概率分布,表示为。
由此,混合策略被定义为给每个纯策略分配一个概率的策略。
混合策略博弈的结果则是一个混合策略纳什均衡(MNE),即每个玩家在给定对手策略不变的情况下选择最优的概率分布。
在混合策略博弈中,期望收益的计算方式也有所改变。
给定策略式博弈和一个混合策略博弈结果,玩家的期望收益是其纯策略博弈结果收益与该结果概率的乘积,对所有结果求和得到。
这体现了混合策略博弈中收益的随机性和不确定性。
混合策略纳什均衡的定义为,当所有玩家选择的混合策略使得每个玩家在对手策略不变的情况下获得最大期望收益时,该混合策略为均衡。
此均衡的存在性是有限策略式博弈的纳什定理的直接结果。
求解混合策略纳什均衡的关键在于确保玩家选择每个具有正概率的纯策略的期望收益相同。
以特定博弈为例,通过构建数学模型,解出玩家选择策略的概率分布,最终得到混合策略纳什均衡。这一均衡的求解体现了博弈论中数学与逻辑的结合,以及解决复杂博弈问题的能力。
总结而言,混合策略的引入为策略博弈中的决策提供了新的维度,不仅解决了纯策略纳什均衡不存在的情况,还为复杂博弈环境中的决策提供了理论基础和实践指导。
在混合策略纳什均衡的框架下,每个玩家在保持稳定局面的同时,确保其对每个策略的期望收益相等,这成为博弈均衡稳定性的关键。









还没有评论,来说两句吧...