纳什均衡理论提出者(纳什的均衡理论)

纳什均衡是博弈论中的一个核心概念，指的是一组策略，在这种策略下，每个参与者都没有动机单独改变自己的策略，因为这样做不会给他们带来更高的收益。这个概念由约翰·纳什提出，是博弈论中的一个重要里程碑。

纳什均衡定义了一种情况，在任何一位玩家改变自己的策略（而其他玩家的策略保持不变）时，他们都不会获得更好的结果。这种均衡点是玩家策略的一种稳定状态，玩家在此状态下没有激励去改变自己的策略。

在博弈论中，一个策略组合被称为纳什均衡，当且仅当每个参与者都选择了在当前情况下最优的策略，并且这个最优策略的选择是考虑到其他所有参与者的策略。

换句话说，纳什均衡是玩家策略的一种平衡，每位玩家都在自己的最佳策略中找到了位置。

约翰·纳什在攻读博士学位期间，对纳什均衡做出了开创性的贡献。

他在1950年发表的论文中，用精确的数学语言定义了纳什均衡，并证明了在有限参与者的博弈中，纳什均衡的普遍存在性。

这一工作不仅区分了合作博弈和非合作博弈，而且对博弈论的发展产生了深远的影响。

纳什均衡的存在性定理和普遍意义的证明，为非合作博弈理论的发展奠定了基础。这一理论不仅扩展了博弈论的应用范围，而且对经济学、政治学、生物学等多个领域产生了广泛的影响。

纳什的均衡理论

纳什均衡是指这样一种均衡：在这一均衡中，每个博弈参与人都确信，在给定其他参与人战略决定的情况下，他选择了最优战略以回应对手的战略。

”也就是说，所有人的战略都是最优的。

而讲解“纳什均衡”的最著名的案例就是“囚徒的困境”。

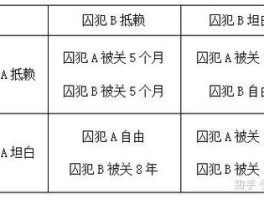
a,b两个囚徒，a坦白b抵赖，b判10年，a判1年.若两人均坦白则各判5年，若两人均抵赖则都判2年。a，b面临抉择。

显然最好的策略是双方都抵赖，结果是大家都只被判2年。

但是由于两人处于隔离的情况下无法串供，按照亚当·斯密的理论，每一个人都是一个“理性的经济人”，都会从利己的目的出发进行选择。

这两个人都会有这样一个盘算过程：假如他招了，我不招，得坐10年监狱，招了才5年，所以招了划算；假如我招了，他也招，得坐5年，他要是不招，我就只坐1年，而他会坐10年牢，也是招了划算。

综合以上几种情况考虑，不管他招不招，对我而言都是招了划算。

两个人都会动这样的脑筋，最终，两个人都选择了招，结果都被判5年刑期。

原本对双方都有利的策略(抵赖)和结局(被判1年刑)就不会出现。这就是著名的“囚徒困境”。它实际上反映了一个很深刻的问题，这就是个人理性与集体理性的矛盾。

对於多人参与、非零和的博弈问题，在纳什之前，无人知道如何求解，或者说怎样找到类似于最小最大解那样的“平衡”。

而找不到解，下面的研究当然无法进行，更谈不上指导实践了。

纳什对博弈论的巨大贡献，正在於他天才性地提出了“纳什均衡”的基本概念，为更加普遍广泛的博弈问题找到了解。

纳什均衡的基本思想是，在这个解集中所有参与者的策略都是对其他参与者所用策略的最佳对策，没有人能够通过单单改变自己的策略提高收益。