弹性模量与杨氏模量的关系(弹性模量与杨氏模量的关系是什么)

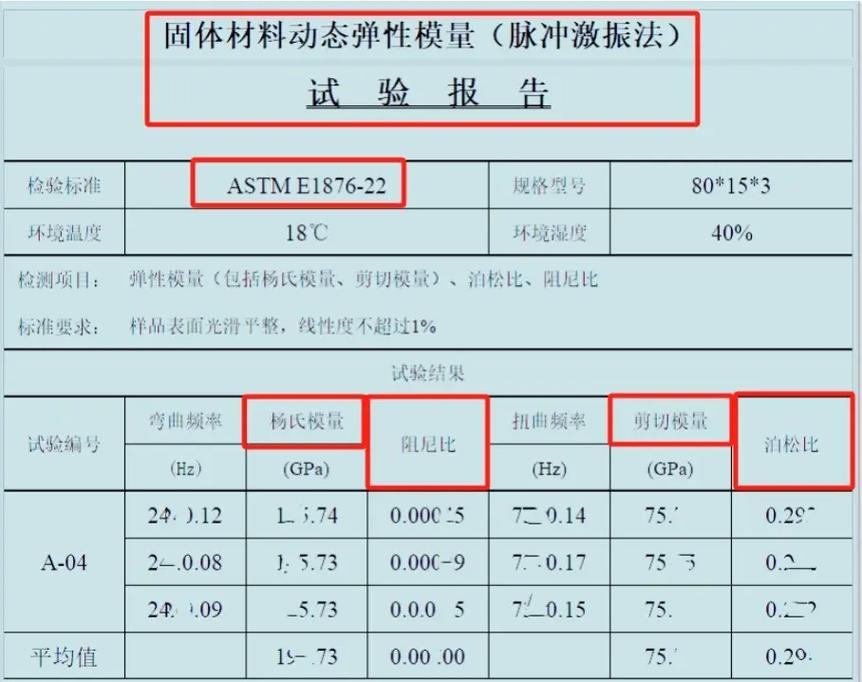
杨氏模量和弹性模量是材料力学中的两个重要参数，它们都是描述材料抵抗弹性变形的能力，但在定义和应用上有所不同。

杨氏模量是描述材料在弹性范围内拉伸或压缩时应力与应变之间的关系的常数。简单来说，它衡量了一个材料在受到外力作用时抵抗变形的能力。杨氏模量越大，材料在受到相同的外力时产生的弹性变形就越小。

弹性模量也是一个反映材料抵抗弹性变形能力的物理量，但它更多地用于描述材料在复杂应力状态下的弹性行为。

弹性模量是一个更广义的概念，它可以包括多种不同类型的应力下的弹性响应。

不同的材料在不同的应力状态下可能有不同的弹性模量值。

两者的主要区别在于其应用范围。

杨氏模量主要是在拉伸或压缩的单一应力状态下使用，更多地应用于金属材料的研究。

而弹性模量则更多地用于描述各种材料在复杂应力状态下的弹性行为，包括但不限于塑料、复合材料等。

此外，不同的材料和行业可能会采用不同的测试方法和标准来测量这两个参数。

总的来说，杨氏模量和弹性模量都是描述材料抵抗弹性变形能力的参数，但在定义和应用上有所不同。杨氏模量主要用于单一应力状态下的弹性行为，而弹性模量则更多地用于描述复杂应力状态下的弹性行为。

弹性模量与杨氏模量的关系是什么

探索材料力学的基石：杨氏模量、弹性模量、剪切模量、体积模量、强度与刚度的深度解析。

在材料科学的世界里，一系列关键参数定义了物体的弹性行为和强度限制。让我们逐一揭开这些术语的神秘面纱：

杨氏模量(Young'sModulus):线性弹性材料的象征，它表示应力与应变之间的直接关系，如钢的杨氏模量约为2×10¹¹N·m^-2，铜则略低，为1.1×10¹¹N·m^-2。

它衡量的是原子间的键合强度以及材料整体的刚度。

弹性模量:这是材料抵抗变形的基础，它是纵向应力与应变的比例，反映了原子间的连接强度和材料的抗形变特性。纵向应力与应变的比值，揭示了材料在受力时的弹性响应。

剪切模量(G):这一参数与杨氏模量并驾齐驱，描述的是材料在剪切力作用下的响应，即剪切应力与剪切应变的比例。它在材料力学中占有重要地位。

体积模量(K):它揭示了材料对压缩的敏感性，等于杨氏模量除以3乘以(1-2ν)，这里的ν即泊松比，反映了材料的横向收缩特性。

压缩模量:与体积模量密切相关，它反映了材料在受压时的应力与应变关系，是理解材料压缩性能的关键指标。

储能模量E'和耗能模量E'':前者代表弹性变形能量的存储，衡量材料回弹性；后者则象征着材料在变形过程中的能量耗散，反映了材料的粘性特性。

切线模量:当材料进入塑性阶段时，切线模量成为衡量增量变形的工具，虽然不是恒定的，但对材料的工程分析至关重要。

截面模量:是构件抵抗弯曲变形的重要参数，它取决于材料的几何形状和中和轴的位置，确保结构在受力时保持稳定。

强度:材料抵抗破裂的能力，包括屈服强度和抗拉强度，是材料性能的基石，受材料组成、微结构和加载方式影响。

刚度:体现材料抵抗变形的能力，衡量的是材料在受力时的弹性响应程度，它与材料性质、截面形状和尺寸紧密相关。

在单轴受力时，我们可以通过胡克定律理解材料的响应，例如，单位应变在X方向引发的Y方向应变比例（b）与在Y方向引发的X方向应变比例（a）之间的关系，通过简单的数学关系得出:。

PRXY/NUXY=EX/EY=b/a(由胡克定律推导)。

这些参数的深入理解，对于材料工程师而言，就如同掌握建筑材料的魔法钥匙，能够构建出既坚固又灵活的结构世界。