黄金分割比例是:0.618:1。
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分比值,其比值约为0.618。这个比例被公认为是最能引起美感的比例,因此被称为黄金分割。
黄金分割又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值为1∶0.618或0.618∶1,即长段为全段的0.618。
0.618被公认为最具有审美意义的比例数字。
在古希腊时期,有一天毕达哥拉斯走在街上,在经过铁匠铺前他听到铁匠打铁的声音非常好听,于是驻足倾听。他发现铁匠打铁节奏很有规律,这个声音的比例被毕达哥拉斯用数学的方式表达出来。
黄金分割点:
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。
其比值是一个无理数,用分数表示为(√5-1)/2,取其前三位数字的近似值是0.618。
由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比例。
这个分割点就叫做黄金分割点(goldensectionratio),通常用Φ表示。
这是一个十分有趣的数字,以0.618来近似表示,通过简单的计算就可以发现:(1-0.618)/0.618≈0.618,即一条线段上有两个黄金分割点。
发展历史:
黄金分割的奇妙之处,在于其比例与其倒数是一样的。
例如:1.618的倒数是0.618,而1.618:1与1:0.618是一样的。
黄金分割点的确切值为是一个无理数,其前100位为:0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374,因此,一般取0.618作为黄金分割点的运算数值。
美学价值:
因为它在造型艺术中具有美学价值,在工艺美术和日用品的长宽设计中,采用这一比值能够引起人们的美感,在实际生活中的应用也非常广泛,建筑物中某些线段的比就科学采用了黄金分割,舞台上的报幕员并不是站在舞台的正中央,而是偏在台上一侧,以站在舞台长度的黄金分割点的位置最美观,声音传播的最好。
就连植物界也有采用黄金分割的地方,如果从一棵嫩枝的顶端向下看,就会看到叶子是按照黄金分割的规律排列着的。
在很多科学实验中,选取方案常用一种0.618法,即优选法,它可以使我们合理地安排较少的试验次数找到合理的西方和合适的工艺条件。
正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用,所以人们才珍贵地称它为"黄金分割"。
黄金分割(GoldenSection)是一种数学上的比例关系。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。应用时一般取0.618,就像圆周率在应用时取3.14一样。
并且人们认为如果符合这一比例的话,就会显得更美、更好看、更协调。
在生活中,对“黄金分割”有着很多的应用。
如:最完美的人体:肚脐到脚底的距离/头顶到脚底的距离=0.618;最漂亮的脸庞:眉毛到脖子的距离/头顶到脖子的距离=0.618。
企业经营管理:
在企业经营管理中,从经验来看,资产负债率(即负债总额除资产总额)应以黄金分割点为临界点,如果高于这个点就可能面临较大经营风险(当然象银行这类企业可以例外),目前正在进行科学论证中。
创造力:
研究人员从拍卖行中选取了200名世界上最著名的艺术家的作品,通过对销售记录进行统计后发现,大部分艺术家创作出最昂贵作品的年龄是在42岁左右,将这个年龄除以他们寿命的平均值后,得数为“0.6198”,这个数字和科学界公认的黄金分割点“0.6180”极为接近。
研究还发现,即使是一些英年早逝的天才,他们也是在自己生命的“黄金分割点”前后创作了自己最伟大的作品。
研究者表示,这项调查中不少艺术家去世年龄较早,可能拉低了最佳年龄的数值,有些艺术家其实是在42岁以后取得非凡成就的。
如毕加索和莫奈分别是在56岁和60岁时创作出了最有价值的作品。
这两位艺术家的巅峰虽然推后了不少,但他们也都是在自己生命的“黄金分割点”前后达到艺术创作顶峰的。
示例
这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。
让我们首先从一个数列开始,它的前面几个数是:1、1、2、3、5、8、13、21、34、55、89、144…。
.这个数列的名字叫做"斐波那契数列",这些数被称为"斐波那契数"。
特点是即除前两个数(数值为1)之外,每个数都是它前面两个数之和。
斐波那契数列与黄金分割有什么关系呢?经研究发现,相邻两个斐波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。
即。
由于斐波那契数都是整数,两个整数相除之商是有理数,所以只是逐渐逼近黄金分割比这个无理数。
但是当我们继续计算出后面更大的斐波那契数时,就会发现相邻两数之比确实是非常接近黄金分割比的。
一个很能说明问题的例子是五角星/正五边形。
五角星是非常美丽的,我们的国旗上就有五颗,还有不少国家的国旗也用五角星,这是为什么?因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的。
正五边形对角线连满后出现的所有三角形,都是黄金分割三角形。
由于五角星的顶角是36度,这样也可以得出黄金分割的数值为2Sin18度。
黄金比例是几比几?
黄金比又称黄金律,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1∶0.618,即长段为全段的0.618。
0.618被公认为最具有审美意义的比例数字。
上述比例是最能引起人的美感的比例,因此被称为黄金分割。
应用在生活中有神奇魅力
这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。在我们生活中比比皆是。
由黄金分割点联想到“黄金分割线”,并类似地给出“黄金分割线”的定义:直线L将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果S1:S=S2:S1,那么称直线L为该图形的黄金分割线。
黄金分割〔GoldenSection〕是一种数学上的比例关系。
黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。
应用时一般取0.618,就像圆周率在应用时取3.14一样。
高雅的艺术殿堂里,自然也留下了黄金数的足迹。
人们还发现,一些名画、雕塑、摄影作品的主题,大多在画面的0.618处。
艺术家们认为弦乐器的琴马放在琴弦的0.618处,能使琴声更加柔和甜美。
黄金矩形(GoldenRectangle)的长宽之比为黄金分割率,换言之,矩形的长边为短边1.618倍。
黄金分割率和黄金矩形能够给画面带来美感,令人愉悦。
在很多艺术品以及大自然中都能找到它。
希腊雅典的巴特农神庙就是一个很好的例子,达·芬奇的《维特鲁威人》符合黄金矩形。
《蒙娜丽莎》中蒙娜丽莎的脸也符合黄金矩形,《最后的晚餐》同样也应用了该比例布局。
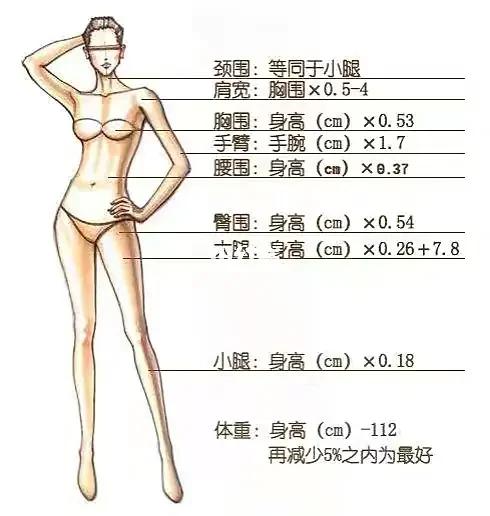
画家们发现,按0.618:1来设计腿长与身高的比例,画出的人体身材最优美,而现今的女性,腰身以下的长度平均只占身高的0.58,因此古希腊维纳斯女神塑像及太阳神阿波罗的形象都通过故意延长双腿,使之与身高的比值为0.618,从而创造艺术美。
难怪许多姑娘都愿意穿上高跟鞋,而芭蕾舞演员则在翩翩起舞时,不时地踮起脚尖。
音乐家发现,二胡演奏中,“千金”分弦的比符合0.618∶1时,奏出来的音调最和谐、最悦耳。
《蒙娜丽莎》是用数字来表示人体美,并根据一定的基准进行比较。
用同一人体的某一部位作为基准,来判定它与体的比例关系的方法被称为同身方法。
分为三组:系数法,常指头高身长指数,如绘画人体比例时是以头为标准的,站是7个头长,坐是5个,蹲是3个;百分数法,将身长视为100%,身体各部位在其中的比例;两分法:即把人体分成大小两部分,大的部分从脚到脐,小的部分为脐到头顶。
标准的面型,其长宽比例协调,符合三庭五眼。
三庭是指脸型的长度,从头部发际到下颏的距离分为三等分,即从发际到眉、眉到鼻尖、鼻尖到下颏各分为一等分,各称一庭共三庭;五眼是指脸型的宽度,双耳间正面投影的长度为五只眼裂的长度,除眼裂外、内此间距为一眼裂长度、两侧外眦角到耳部各有一眼裂长度。








还没有评论,来说两句吧...