通用图灵机(通用图灵机的概念)

图灵机的正确说法如下：

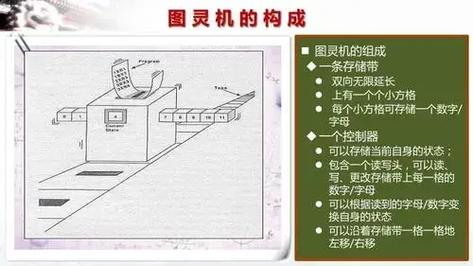
图灵机是一种抽象的计算机模型，不具备实际的物理形态。图灵机有一个无限长的纸带，用于存储和处理信息。纸带被分成一个个小格子，每个格子可以存储一个符号。

图灵机有一个读写头，可以在纸带上左右移动，读取或写入符号。图灵机的操作是由一个控制规则表来定义的，该表根据当前读写头所读取的符号以及当前的状态来决定下一步的操作。

图灵机是一种通用计算模型，可以模拟任何算法的计算过程。

图灵机的概念奠定了现代计算机科学的基础，对于计算机科学的发展产生了深远的影响。

图灵机是一种非常重要的理论计算模型，它不仅奠定了现代计算机科学的基础，也为人工智能、计算复杂性等领域的研究提供了重要的工具。

图灵机的操作方式：

1、写操作：图灵机可以通过写操作将指定的符号写入纸带上的一个格子中。

这个操作通常是在图灵机的起始状态下进行的，用于在纸带上存储初始的输入信息或程序代码。

写操作是图灵机最基本的操作之一，使得图灵机能够将信息存储在纸带上并进行处理。

2、读操作：图灵机可以通过读操作读取当前格子中的符号。这个操作通常是在图灵机的运行状态下进行的，用于获取当前处理的符号信息。读操作使得图灵机能够读取纸带上的信息，并根据读取到的符号来执行相应的操作。

3、转移操作：图灵机可以通过转移操作将读写头从一个格子移动到另一个格子。

这个操作通常是在图灵机的运行状态下进行的，用于控制读写头在纸带上的移动。

转移操作的实现依赖于控制规则表，根据当前读取到的符号以及当前的状态来决定下一步的操作，包括读写头向右移动一格、向左移动一格或者停留在当前格子等。

通用图灵机的概念

这几年由于区块链的大热，以太坊独特的solidity语言实现智能合约功能，图灵完备这个词走进大家的视线。

没有计算机专业知识的同学其实很难理解这个词的意思，其实计算机专业的同学都没有深入理解图灵机，图灵完备，图灵测试等概念包含的内涵。

为了方便理解区块链技术，理解智能合约，笔者准备分几篇文章来带大家从浅入深，一步一步带你深入理解图灵机，相信通过这几篇文章能就能够理解什么是图灵完备。

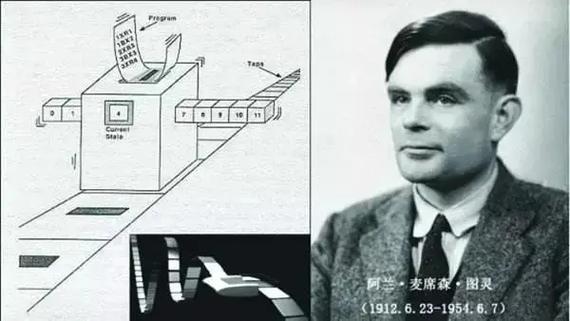
艾伦·麦席森·图灵（AlanMathisonTuring，1912年6月23日－1954年6月7日），英国数学家、逻辑学家，被称为计算机科学理论之父，人工智能之父。

1931年，图灵考入剑桥大学国王学院，由于成绩优异而获得数学奖学金。

1936年5月，年仅24岁的图灵发表一篇题为《论数字计算在决断难题中的应用》的论文，论文中提出一种计算装置，后被称为“图灵机”，图灵机不是具体的计算机，而是一种计算概念、计算理论。

1938年在普林斯顿获博士学位，其论文题目为“以序数为基础的逻辑系统”，在数理逻辑研究中产生了深远的影响；同年图灵回到英国，在剑桥大学国王学院任研究员。

第二次世界大战期间，1939年图灵到英国外交部通信处从事军事工作，主要是破译敌方密码的工作。

由于破译工作的需要，他参与了世界上最早的电子计算机的研制工作。

他的工作取得了极好的成就，破译了德国人Enigma密码，于1945年获政府的最高奖——大英帝国荣誉勋章。

1945年，图灵结束了在外交部的工作，他试图恢复战前在理论计算机科学方面的研究，具体研制出新的计算机来。

1950年他发表论文《计算机器与智能》（ComputingMachineryandIntelligence），为后来的人工智能科学提供了开创性的构思。提出著名的图灵测试。

1950年，1950年10月，图灵发表论文《机器能思考吗》。

这一划时代的作品，使图灵赢得了“人工智能之父”的桂冠。

此时，人工智能也进入了实践研制阶段。

随着这几年AI技术的不断成熟，人们越来越认识到图灵思想的深刻性：它们至今仍然是人工智能的主要思想之一。

1954年6月7日，年仅41岁的图灵被发现死于家中的床上，床头还放着一个被咬了一口的苹果。这就是现在大名鼎鼎的苹果电脑公司logo的来源。

从图灵的生平中，我们知道，他出生在20世纪初，1912年。

在世界国家格局上，这个时候刚刚爆发第一次世界大战（1913~1921），紧接着1939年至1945年第二次世界大战，大家知道，这两次世界大战倒逼了很多科技的发展，二战期间恰好是图灵青年时代。

在科技文明发展上，由于逻辑的数学化，促使了数理逻辑学科的诞生和发展。

但同时这个时期数学上发生了第三次数学危机，具体介绍在下方。

图灵在剑桥读大学期间，修读了“数学基础”课程，授课人是纽曼，纽曼整个课程包含对哥德尔不完备性定理的证明和尚未解决的判定性问题。

这些科技事件的背后，其实是人们在认知上，对可计算性理论的研究，图灵正是这个问题终结者。

随便提一下，爱因斯坦1905年提出狭义相对论，1927年年仅15岁的图灵为了帮助母亲理解相对论，还写过论文的摘要。

在20世纪以前，人们普遍认为，所有的问题类都是有算法的，人们的计算研究就是找出算法来。1900年，当时著名的大数学家希尔伯特在世纪之交的数学家大会上给国际数学界提出了著名的23个数学问题。

其中第十问题是这样的：

“丢番图方程”指：有一个或者几个变量的整系数方程，它们的求解仅仅在整数范围内进行。

上面这个问题简单点解释是：随便给一个不确定的方程，是否通过有限的步骤运算，判断这个方程是否存在整数解。

这个问题在1970年，苏联一个数学家证明了其实很多数学问题，是没有答案，甚至没有答案的问题比有答案的问题还要多。

这里就提出来了有限的、机械的证明步骤的问题，其实就是算法。

但在当时，人们还不知道“算法”是什么。

实际上，当时数学领域中已经有很多问题都是跟“算法”密切相关的，因而，科学的“算法”定义呼之欲出。

之后到了30年代的时候，终于有两个人分别提出了精确定义算法的方法，一个人是图灵，一个人是丘奇。

而其中图灵提出来的图灵机模型直观形象。

图灵思考这个问题的方式和常人不一样，在写前面提到的论文《论可计算数及其在判定性问题上的应用》的时候，图灵在思考三个问题。

图灵这样的天才考虑问题的认知是高屋建瓴的。

图灵首先考虑的是是否所有数学问题都用解，如果这个问题不解决，辛辛苦苦解题，最后发现无解，一切的努力都是浪费时间和精力。

对于存在答案的数学问题，只有部分是可以在有限步骤内完成，这样把计算机的边界确定下来了。

确定了边界之后，就要设计一种通用、有效、等价的机器，保证可以按照这个方法做事，最后得到答案。而图灵机就是图灵设计出来的这样的一个机器，严格来讲是一种数学模型、计算理论模型。

从图灵机提出到现在已经过去了80多年，今天所有的计算机，包括量子计算机都没有超出图灵机的理论范畴。

第三次数学危机产生于十九世纪末和二十世纪初，当时正是数学空前兴旺发达的时期。首先是逻辑的数学化，促使了数理逻辑这门学科诞生。

早在19世纪末的时候，康托尔为集合论做了奠基性的研究。

人们发现，运用集合这个概念可以概括所有的数学，也就是说集合是一切数学的基础。

然而就当这座大厦即将完工的时候，一件可怕的事情发生了，罗素提出来的罗素悖论粉碎了数学家的梦想。

关于罗素悖论的一个通俗化版本是：

第二次工业革命主要电和磁、内燃机的发明和使用，发展到这个时候科学家对世界的认知越来越多，越来越清晰，物理学和数学等自然科学发展迅速。

这个时候的数学家发现很多现象可以用数学模型来表示，从物体的运动到星球的运动、从热能到动能的转换、从电到磁的转换等等。

那问题来了是否所有的现象都可以用数学模型来表达呢？真是这个问题，让人们对数学很多根本性问题进行思考和研究。

中国有句古话说：乱世出英雄。

在图灵的时代，在科学历史上出了很多的科学英雄，包括爱因斯坦、冯诺依曼、图灵、哥德尔等等，一方面是时代背景使然，一方面真是他们的天赋和努力让以信息化为代表的第三次工业革命的进程大大加快了。

从这些巨匠的思考问题，解决问题的方法和认知来看是超出常人的。从对可计算性理论的思考，给了我们很大的启示：

**更多有关区块链的技术与思维，可扫码加入我的小密圈。在这里，我陪着你，大家一起研究区块链技术，探讨区块链思维，预测区块链未来，一起做未来前10%的人。

**