图灵机是什么样的

冯·诺伊曼结构（vonNeumannarchitecture），也称普林斯顿结构，是一种将程序指令存储器和数据存储器合并在一起的电脑设计概念结构。

本词描述的是一种实作通用图灵机的计算装置，以及一种相对於平行计算的序列式架构参考模型（referentialmodel）。

本架构隐约指导了将储存装置与中央处理器分开的概念，因此依本架构设计出的计算机又称储存程式型电脑。

……文章的后面写：

毛奇利（Mauchly）与艾克特（Eckert）在1943年於他们建造ENIAC时写下关於储存程式的概念，另外，ENIAC计画管理员布莱德（GristBrainerd）在1943年12月为ENIAC做的进度回报，就已隐约提及储存程式的概念（虽然也同时否决了在ENIAC实作的计画），他说「为了拥有最简单的实作计画以及不复杂的事务，ENIAC建造时后将不需要任何自动整备」。

当设计ENIAC时，它很清楚说明从读卡机或纸带读取指令是不够快的，因为ENIAC设计用於高速执行运算。

因此ENIAC直接以电路管线设计程式，并在需要新程式时重新配接线路。

设计师也很清楚他们需要更好的系统架构，因此在ENIAC建造期间第一份EDVAC的报告就已撰写完毕，并包含了储存程式的概念，此概念叙述程式指令储存在高速记忆体（水银延迟记忆体）中，因此可以在执行时快速存取。

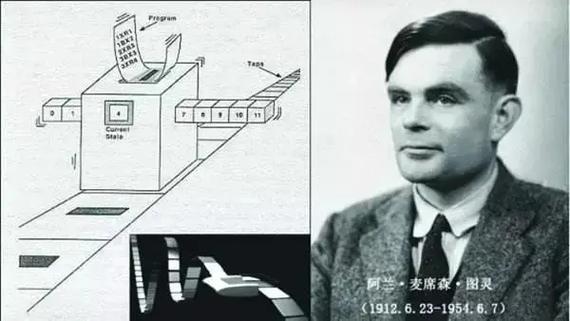
图灵机是用来干什么的

图灵机是形式化定义的计算模型，由一个七元组组成。

在计算时，图灵机将状态、带子内容和读写头当前位置组合成一个Configuration。

配置转移表示图灵机的计算过程。

例如，如果状态为[公式]，当前读写头指向符号b，且左右字符串分别为[公式]，则称其为Configuration。

若状态和符号满足一定条件，图灵机可以从一个Configuration转移到另一个。

配置序列描述了输入被图灵机处理的过程。

图灵机的变种包括多带图灵机与单带图灵机，两者在功能上等价。

非确定性图灵机在决策路径上允许多条可能的转移，当且仅当有一条路径使其进入接受状态时接受输入。

与确定性图灵机相比，非确定性图灵机的决策过程构成一棵决策树，深度可能无限，因此不能用深度优先遍历来模拟，而是使用宽度优先遍历。

在非确定性图灵机模拟中，使用特定字符表示动作，动作集合可表示为字符串。

输入被记录在第一条纸带上，第二条纸带模拟给定选择地址串下的纸带变化。

第三条纸带用来记录地址。

模拟过程在有限时间内进行，若在模拟后未进入接受状态则放弃当前输入，刷新第二条纸带内容并继续循环模拟。

Church-TuringThesis认为，算法的直观概念与图灵机算法等价。

希尔伯特第十问题探讨了多项式方程组的可判定性，证明了对于某些方程组，不存在可判定算法。

对于一维情形，遍历算法可以转化为判定器。

然而，Matijasevic定理表明，对于多变元多项式方程组计算上界是不可能的，因此无法确定算法是否停机。