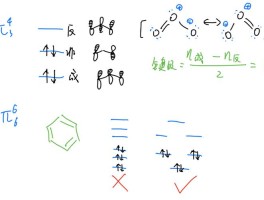
量子力学基石:泡利不相容原理
沃尔夫冈·泡利的这一理论犹如一道闪电,揭示了微观世界中一个核心法则——泡利不相容原理。
它断言,两个全同的费米子,如电子,无法共享同一组完整的量子参数:主量子数揭示能量层次,角量子数决定轨道特性,磁量子数与自旋磁量子数共同定义了独特的粒子特性。
在某个能级上,即使是最小的空间,也只能容纳两个自旋相反的电子,犹如宇宙间的一对量子舞者,各占一方。
费米-狄拉克统计:粒子世界的隐形规则
费米-狄拉克统计,如同宇宙的隐形指南针,指导着费米子如何在微观世界中分布。
这源于两位科学巨擘的洞察力——恩里科·费米和保罗·狄拉克,他们的名字成为这一统计律的象征。
它规定了粒子如何在遵循泡利不相容原理的系统中,理智地占据各自的量子空间,形成独特的统计规律,塑造了金属等物质的奇异行为。
索末菲的贡献与金属电子理论的深化
1927年,阿诺·约翰内斯·威廉·索末菲将费米-狄拉克统计引入金属电子理论,与保罗·德劳德的理论相结合,诞生了Drude-Sommerfeld模型。
这个革命性的模型修正了原始理论对金属热性能的预测,为我们理解金属世界的电子行为提供了全新的视角。
费米能级:微观世界里的电子舞台
费米能级,这个神秘的量子标尺,标志着电子填充的最高能量界限。
在零度时,电子按照能量最低原则填充,形成球形的Fermi球面,每个能级最多容纳两个自旋相反的电子。
费米能级不仅是电子填充的终点,也是温度上升时电子行为变化的关键转折点。
温度与费米能级的互动
当温度升高,费米能级并非一成不变,它随着温度的变化而调整。
在非零温度下,费米能级会低于低温状态下的基态值,呈现出独特而微妙的温度依赖性。
这些变化揭示了费米气体在宏观世界中的量子特性,是理解金属导电性和热导性的关键。
费米气体和费米液体
20世纪20-30年代,Bethe、Sommerfeld、Bloch等人建立的能带理论揭示了金属与绝缘体的本质区别。
然而,对部分d电子能带的过渡金属氧化物(如NiO)的实验结果显示,这类系统表现出较差的导电性,而不是能带理论预测的金属。
Peierls指出,电子间的强Coulomb排斥力是导致这种绝缘行为的原因。
Mott提出了关键理论,考虑了每个晶格点具有单个电子轨道的模型(单带Hubbard模型)。
在无电子相互作用时,电子轨道间的重叠会导致能带形成。
当每个格点被自旋上与自旋下电子同时占据时,能带被填满。
但当两个电子占据同一个格点时,会感受到巨大的Coulomb排斥力,导致能带分裂为两个:下能带由占据空格点的电子形成,上能带由已被一个电子占据的格点上再占据一个电子所形成。
当每个格点平均有一个电子时,下能带被填满,系统成为绝缘体。
我们通常将这类讨论的由电子相互作用诱导的绝缘体称为Mott绝缘体。
注意到Mott理论未涉及系统是否具有磁性。
若金属与Mott绝缘体之间发生相变,则称为Mott相变。
除了过渡金属氧化物,4f和5f化合物也与Mott物理相关,严格地说,f电子体系应被视为轨道选择的Mott体系。
人工合成结构如转角石墨烯、超冷原子气体和受限离子体系也是模拟和观测Mott物理的典型系统。
与Mott理论不同,Slater将系统中的绝缘行为归因于磁性有序,如反铁磁长程序。
物理上,Slater认为系统首先出现反铁磁有序,随后反铁磁序导致电子能带折叠,形成两支准粒子能带。
当电子填满低能准粒子能带,体系在一定条件下成为绝缘体。
这类绝缘体称为Slater绝缘体。
与之相对,Mott绝缘体首先由于电子关联而从顺磁性金属转变为顺磁性绝缘体,然后通过降温等方式转变为反铁磁的绝缘体。
显然,Slater绝缘体与Mott绝缘体从绝缘的本质来看并不相同。
实验上,大多数Mott绝缘体在零温(低温)下具有反铁磁性有序,从Slater的解释来看,这些绝缘体看起来像是一个能带绝缘体,能隙由磁有序的周期性导致的超晶格结构所产生。
然而,实验结果支持Mott绝缘体的解释,即绝缘性来自关联而非能带填充。
针对狭义的Mott相变,当相变为连续的或弱的一级相变时,预计在从金属态接近相变点时,金属态中自旋、电荷以及轨道关联的涨落会变得很强。
这些强烈的涨落强烈影响金属行为,例如通过比热和磁化率测量发现有效质量得到相当大的增强。
为了理解这种质量增强,Brinkmann和Rice利用Gutzwiller近似研究Hubbard模型,并发现Mott相变附近的金属态中电子质量确实有很大的增强。
热容、磁化等物理量正确反应这种质量增强效应。
事实上,他们的近似仅用于Mott相变的金属态一边,描述的仅是相干的准粒子的贡献,而非相干的贡献。
早期的Mott相变研究可以概括为:一个更为完整的Mott相变理论应该包含Hubbard近似与Gutzwiller近似的主要特性,即从电子谱的角度来说需要有上下Hubbard能带与准粒子能带。
从方法论的角度来看,研究Mott相变的理论方法主要有动力学平均场理论(DMFT)、辅助粒子技术、量子蒙特卡洛模拟(行列式蒙特卡洛或变分蒙特卡洛)和基于张量的方法(如密度矩阵重整化群、矩阵乘积态、张量重整化)。
在这里,我们主要介绍最流行且被研究者们广泛认可的动力学平均场理论。
动力学平均场理论(DMFT)方法成功地将Hubbard近似与Gutzwiller近似的核心特性结合在一起,成为理解Mott相变的标准工具。
对于DMFT,其含义是通过动力学平均场近似,我们仅讨论一个格点上的电子问题,该电子既受到格点内的相互作用,也会感受到其他格点电子形成的有效场对它的影响。
通过求解这个等效的杂质问题,我们可以得到该格点电子的相互作用修正,即自能。
假定每一个格点都是等价的,那么其他格点上的电子也会有一样的自能,因此它们在该自能修正后的行为与我们关注的格点行为相同。
这就得到一个自洽理论,数学上相当于存在一系列自洽的积分方程,通过求解方程可以得到系统的行为,例如电子的态密度和谱函数。
电子间的相互作用已经由所有电子的贡献进行平均,因此数学上来看电子的自能函数仅是频率的函数而不显示空间依赖(没有动量的依赖关系),即自能是空间局域的。
值得注意的是,全息对偶/规范-引力对偶发现的非费米液体也具有类似的局域自能,这是近黑洞视界的必然结果。
具体而言,对于Hubbard模型,如果关注于某个格点,例如第零格点,那么我们可以把其他格点作为这个格点的有效场或环境看待。
通过路径积分形式,我们积掉环境自由度,得到第零格点的动力学。
在动力学平均场的背景下,体系的配分函数可以表示为作用量形式,通过路径积分推导动力学平均场时,我们采用所谓的腔方法(cavitymethod)。
首先,体系的配分函数可用作用量表示为。
在统计物理中,我们通常对相互作用部分做指数展开,然后逐项计算,这就是传统的微扰展开。
然而,在这里如果我们直接展开,无法得到Mott物理。
因此,我们改为展开项,即。
这样配分函数可以写成。
这里定义了。
原则上,我们需要考虑关于无穷阶的贡献,但这明显不现实。
不过注意到我们是以作为参考进行展开,这相当于是做了强耦合展开,也就是以作为展开参数,在时可以忽略所有的高阶项。
另一方面,如果我们重标,这样重标可以使得在获得行为良好的自由电子态密度。
这里是系统的空间维度,那么展开的第项正比于,这样在也就是所谓的无穷维极限下只需要考虑和这两阶。
因此有。
注意到对于粒子数守恒的系统,单粒子平均必然为零,即或说由于我们是对奇数个费米子做Grassman数积分,其必定为零。
这说明与环境的一阶耦合项为零,实际上所有奇数次项都为零。
因此,我们需要计算二阶项。
通过这个过程,我们可以得到单格点问题的Green函数和有效作用量,从而更好地理解Mott相变的物理过程。
DMFT理论的核心是计算任意参数下的虚拟Anderson杂质模型。
在实际操作中,我们可以先猜测一个,这对应于一组确定的,然后利用数值或解析的方法计算Anderson杂质模型的Green函数,再根据公式得到自能。
再把代入公式得到,最后利用和以及获得新的,重复此循环直到Green函数收敛就求解了DMFT方程。
通过DMFT理论计算,我们可以得到单带Hubbard模型态密度()的典型结果,即随着的逐渐增加,系统经历金属-绝缘体相变,上下Hubbard能带出现并伴随着费米能附近准粒子态密度的抑制(准粒子峰变窄最后消失)。
这种态密度的行为可以通过相应的Anderson杂质模型来理解。
因为系统通过DMFT映射为自洽环境(热库)下的Anderson杂质模型,当环境(热库)类似于自由费米气体时,Anderson磁性杂质自然在低温下被屏蔽,显示费米能附近的Kondo共振峰,这就是费米液体态时的中心准粒子峰,此时磁性杂质的自旋时完全屏蔽的,系统处于非简并的状态。
当相互作用足够大,使得环境(热库)态密度在费米能附近为零时,Kondo共振不会发生,磁性杂质并未被屏蔽,因而费米能附近的态密度消失,而系统处于Mott绝缘态,每个格点的电子自旋都未被屏蔽,系统总体显示巨大的自旋简并。
这种巨大简并可以通过超越DMFT的修正而导致的磁性有序态来消除。
从理论上来说,DMFT已被关联电子系统领域的研究者所接受,至少在无穷维(空间维度)和大配位数条件下是精确的。
目前,人们认为该类方法定性或者半定量地抓住了Mott相变的基本物理,在电子性质主要由频率而非动量决定的情况下是一个可靠的近似,对于一些实际材料也可以给出合理的数值估计,因此与密度泛函理论结合成为当前材料电子结构计算的最有力方法。
然而,DMFT对空间做了平均化处理,而我们知道自旋自由度的涨落在空间尺度上总是重要的。
因此,DMFT理论并不能用来研究Mott相变相关的低能磁性质。
当前并没有哪一种方法可以同时研究Mott相变的高能电子结构和低能的磁性激发。
在实际研究中,往往是通过DMFT得到顺磁态的电子能带和谱信息,然后通过半唯象的方式构造低能自旋或轨道自由度的有效模型,对这些模型采用进一步的解析或数值方法进行研究。
DMFT适合于研究能量较高的电子谱和能带结构,不适用于低能的磁性激发和其他集体激发。
如果在Hubbard模型基础上考虑反铁磁Heisenberg交换并采用隶自旋表示,然后再用DMFT研究,会发现低温下体系会从费米液体金属发生一级相变而进入自旋液体态,高温下的性质与自旋液体无关而与通常Hubaard模型的DMFT符合,因此高温下在一级相变临界终点附近的临界性质是Mott物理自身的特性而与自旋液体无关。
一个有趣的DMFT工作研究了无穷维Bethe晶格上单带Hubbard模型的Mott相变。
他们的研究表明Mott相变可以看作是一类拓扑相变。
通过把DMFT自能用辅助的等效SSH模型代替,人们发现Mott态对应SSH模型的拓扑态,也就是有robust边界态的情况,而费米液体态则对应SSH的拓扑平凡态,相变则是SSH模型中畴壁的溶解。
对于Hubbard模型,人们发现其动力学平均场所得Mott态满足。
这里考虑了自旋简并因子,动力学平均场的自能仅是频率的函数以及是动量平均后的Green函数。
其中对于费米液体态和粒子-空穴对称的Mott态成立,而对于不具有粒子-空穴对称的Mott态成立。
这说明,Luttinger积分可以看作是一种刻画非对称Mott态的拓扑的序参量。








还没有评论,来说两句吧...