关于图灵机的说法,错误的是图灵机只能处理离散的数据。
图灵机是由英国数学家艾伦·图灵于1936年提出的一种抽象计算模型,它是一种理论上能够模拟任何计算机程序的计算机。
图灵机可以处理离散和连续的数据。
在图灵机的设计中,纸带上的格子可以被看作是离散的数据,每个格子可以包含一个特定的符号。
图灵机也可以通过模拟实数运算来处理连续的数据。
例如,可以将一个实数表示为一个无限小数,然后用图灵机来模拟这个实数的四则运算。
虽然图灵机是一种理论上的计算机模型,但它对计算机科学的发展产生了深远的影响。
图灵机的概念奠定了现代计算机的理论基础,它被认为是计算机科学的奠基之作之一。
通过图灵机的设计,人们可以更深入地理解什么是可计算的,什么是不可计算的,以及计算机的能力和限制。
图灵机的应用场景:
1、算法设计与分析:图灵机是理解和设计算法的重要工具。很多经典的算法,如图论算法、排序算法、搜索算法等,都可以用图灵机来描述和实现。图灵机也是分析算法复杂性和可计算性的重要工具。
2、人工智能与机器学习:在人工智能和机器学习领域,图灵机也有着广泛的应用。
例如,可以用图灵机来描述和实现各种机器学习算法,如神经网络、决策树、支持向量机等。
图灵机也可以用于分析和理解人工智能系统的性质和限制。
3、逻辑与哲学:在逻辑和哲学领域,图灵机也有着重要的应用。例如,可以用图灵机来描述和实现各种逻辑系统和哲学理论,如模态逻辑、道义逻辑、认知逻辑等。图灵机也可以用于分析和理解逻辑和哲学的基本概念和原理。
4、形式语言与自动机理论:在计算机科学中,形式语言与自动机理论是研究计算模型、计算复杂性和计算性质的重要领域。图灵机作为最重要的计算模型之一,在该领域中扮演着至关重要的角色。
图灵机是什么机器对吗
图灵机
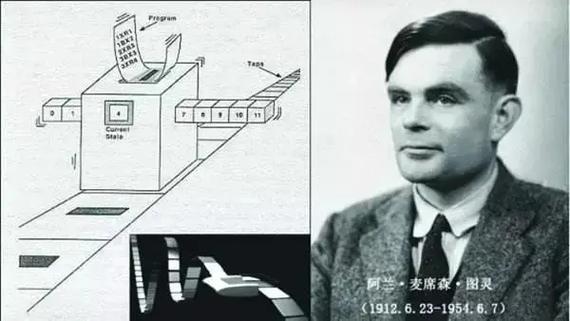
1936年,阿兰·图灵提出了一种抽象的计算模型——图灵机(TuringMachine)。图灵的基本思想是用机器来模拟人们用纸笔进行数学运算的过程,他把这样的过程看作下列两种简单的动作:
在纸上写上或擦除某个符号;
把注意力从纸的一个位置移动到另一个位置;
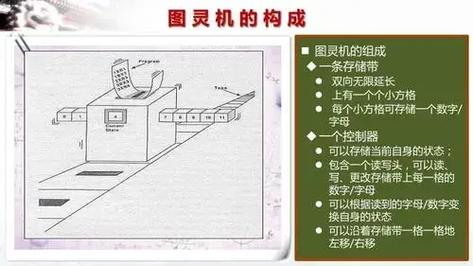
而在每个阶段,人要决定下一步的动作,依赖于(a)此人当前所关注的纸上某个位置的符号和(b)此人当前思维的状态。为了模拟人的这种运算过程,图灵构造出一台假想的机器,该机器由以下几个部分组成:
一条无限长的纸带。纸带被划分为一个接一个的小格子,每个格子上包含一个来自有限字母表的符号,字母表中有一个特殊的符号表示空白。纸带上的格子从左到右依此被编号为0,1,2,...,纸带的右端可以无限伸展。
一个读写头。该读写头可以在纸带上左右移动,它能读出当前所指的格子上的符号,并能改变当前格子上的符号。
一个状态寄存器。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的,并且有一个特殊的状态,称为停机状态。
一套控制规则。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作,并改变状态寄存器的值,令机器进入一个新的状态。
注意这个机器的每一部分都是有限的,但它有一个潜在的无限长的纸带,因此这种机器只是一个理想的设备。图灵认为这样的一台机器就能模拟人类所能进行的任何计算过程。
自动机
automata
对信号序列进行逻辑处理的装置。
在自动控制领域内,是指离散数字系统的动态数学模型,可定义为一种逻辑结构,一种算法或一种符号串变换。
自动机这一术语也广泛出现在许多其他相关的学科中,分别有不同的内容和研究目标。
在计算机科学中自动机用作计算机和计算过程的动态数学模型,用来研究计算机的体系结构、逻辑操作、程序设计乃至计算复杂性理论。
在语言学中则把自动机作为语言识别器,用来研究各种形式语言。
在神经生理学中把自动机定义为神经网络的动态模型,用来研究神经生理活动和思维规律,探索人脑的机制。
在生物学中有人把自动机作为生命体的生长发育模型,研究新陈代谢和遗传变异。
在数学中则用自动机定义可计算函数,研究各种算法。
现代自动机的一个重要特点是能与外界交换信息,并根据交换得来的信息改变自己的动作,即改变自己的功能,甚至改变自己的结构,以适应外界的变化。
也就是说在一定程度上具有类似于生命有机体那样的适应环境变化的能力。
自动机与一般机器的重要区别在于自动机具有固定的内在状态,即具有记忆能力和识别判断能力或决策能力,这正是现代信息处理系统的共同特点。
因此,自动机适宜于作为信息处理系统乃至一切信息系统的数学模型。
自动机可按其变量集和函数的特性分类,也可按其抽象结构和联结方式分类。
主要有:有限自动机和无限自动机、线性自动机和非线性自动机、确定型自动机和不确定型自动机、同步自动机和异步自动机、级联自动机和细胞自动机等。











还没有评论,来说两句吧...